Question

如图，若P是边长为a的等边△ABC内的任一点，P到三边的距离为PD、PE、PF，求证：
（1）PD+PE+PF=

3

2

a
（2）AD+BE+CF=

3

2

a．

Answer 1

考点：等边三角形的性质

专题：证明题

分析：（1）连接PA、PB、PC，则△ABC被分割成三个三角形，根据S_△PAB+S_△PBC+S_△PAC=S_△ABC，即：

1

2

a•PD+

1

2

a•PE+

1

2

a•PF=

3

4

a²，可得PD+PE+PF=

3

2

a；
（2）根据勾股定理得：BE²+PE²=PB²=BF²+PF²①，CF²+PF²=PC²=CD²+PD²②，AD²+PD²=PA²=AE²+PE²③，再由①+②+③得出BE²+CF²+AD²=BF²+CD²+AE²，整理后即可得出结论．

解答：证明：（1）连接PA、PB、PC，则△ABC被分割成三个三角形，如图所示：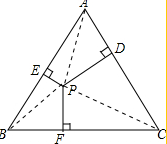
∵S_△PAB+S_△PBC+S_△PAC=S_△ABC，S_△ABC=

3

4

a²，BE²+CF²+AD²=BF²+CD²+AE²，
即：

1

2

a•PD+

1

2

a•PE+

1

2

a•PF=

3

4

a²，
∴PD+PE+PF=

3

2

a；
（2）根据勾股定理得：
BE²+PE²=PB²=BF²+PF²①，
CF²+PF²=PC²=CD²+PD²②，
AD²+PD²=PA²=AE²+PE²③，
①+②+③得：BE²+CF²+AD²=BF²+CD²+AE²，
∴BE²+CF²+AD²=（a-CF）²+（a-AD）²+（a-BE）²=（a²-2CF•a+CF²）+（a²-2AD•a+AD²）+（a²-2BE•a+BE²）
整理得：2a（AD+BE+CF）=3a²
∴AD+BE+CF=

3

2

a．

点评：本题考查了等边三角形的性质、三角形面积的计算方法以及勾股定理的运用；本题综合性强，难度很大，有利于培养学生钻研和探索问题的精神．