题目内容
9.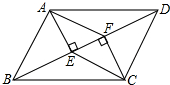 如图,在?ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断
如图,在?ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断(1)△ABE和△CDF全等吗?请说明理由;
(2)四边形AECF是不是平行四边形,并说明理由.
分析 (1)根据平行四边形的性质,可得AB与CD的关系,根据平行线的性质,可得∠ABE=∠CDF,根据AAS,可得答案;
(2)根据平行线的判定,可得AE与CF的关系,根据全等三角形的判定与性质,可得AE与CF的大小关系,根据平行四边形的判定,可得答案.
解答 解:(1)△ABE≌△CDF,理由如下:
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AEF=∠CFE=90°.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
在△ABE与△DCF中,$\left\{\begin{array}{l}{∠ABE=∠CDF}\\{∠AEF=∠CFE}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△CDF(AAS);
(2)四边形AECF是平行四边形.
理由如下:∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AEF=∠CFE=90°,
∴AE∥CF(内错角相等,两直线平行),
在平行四边形ABCD中,AB=CD,AB∥CD,
∴∠ABE=∠CDF,
在△ABE与△DCF中,$\left\{\begin{array}{l}{∠ABE=∠CDF}\\{∠AEF=∠CFE}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△CDF(AAS),
∴AE=CF,
∴四边形AECF是平行四边形(有一组对边平行且相等的四边形是平行四边形).
点评 本题考查了平行四边形的判定与性质,利用;利用平行四边形的性质,全等三角形的判定与性质,平行四边形的判定,熟记平行四边形的判定与性质是解题关键.

练习册系列答案
相关题目
19.若代数式x2+3x+2可以表示为(x-1)2+a(x-1)+b的形式,则a+b的值是( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
20.在-$\frac{π}{3}$,3.1415,0,-0.333…,-$\frac{22}{7}$,-0.$\stackrel{•}{1}$$\stackrel{•}{5}$,2.010010001…中,有理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
1.若多项式2x2-3x+1的值是6,则6x2-9x+5的值是( )
| A. | 18 | B. | 16 | C. | 15 | D. | 20 |
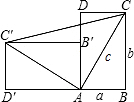 一个直立的火柴盒在桌面上倒下,启迪人们发现快乐勾股定理的一种新的证明方法,如图所示,火柴盒的一个侧面ABCD倒下到A′B′C′D′的位置,连接CC′.设AB=a,BC=b,AC=c,请利用此图证明勾股定理:a2+b2=c2.
一个直立的火柴盒在桌面上倒下,启迪人们发现快乐勾股定理的一种新的证明方法,如图所示,火柴盒的一个侧面ABCD倒下到A′B′C′D′的位置,连接CC′.设AB=a,BC=b,AC=c,请利用此图证明勾股定理:a2+b2=c2.