题目内容

19．若代数式x2+3x+2可以表示为（x-1）2+a（x-1）+b的形式，则a+b的值是（　　）
A．10B．11C．12D．13

分析 利用x2+3x+2=（x-1）2+a（x-1）+b，将原式进行化简，得出a，b的值，进而得出答案．

解答 解：∵x2+3x+2
=（x-1）2+a（x-1）+b
=x2+（a-2）x+（b-a+1），
∴a-2=3，
∴a=5，
∵b-a+1=2，
∴b-5+1=2，
∴b=6，
∴a+b=5+6=11，
故选：B．

点评 此题主要考查了整式的混合运算与化简，根据已知得出x2+3x+2=x2+（a-2）x+（b-a+1）是解题关键

练习册系列答案
相关题目
9．下列几何体中，截面不可能为三角形的是（　　）
A．圆锥B．长方体C．球D．五棱柱
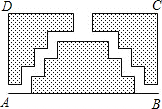10．如图是一块长方形ABCD的场地，长AB=（3a+2）米，宽AD为（a+1）米，从A、B两处入口的小路宽都为1米，两小路汇合处路宽为2米，其余部分种植草坪，则草坪面积为3a2 平方米．
7．计算
①4×（-3）2-5×（-2）3+6         
②（-2$\frac{1}{3}$）-$\frac{5}{6}$+（-0.5）-（-1$\frac{1}{6}$）
③$（\frac{1}{2}+\frac{1}{3}-\frac{1}{6}+\frac{1}{8}）×（-24）$
④（-1）3×（-5）÷[（-3）2+2×（-5）]
⑤49$\frac{19}{21}$+（-78.21）-（-27$\frac{2}{21}$）+（-21.79）
⑥（-4）203×（0.25）204
⑦${（-3）^2}-{（1\frac{1}{2}）^3}×\frac{2}{9}-6÷|-\frac{2}{3}{|^3}$
⑧|$\frac{1}{10}$-$\frac{1}{11}$|+|$\frac{1}{11}$-$\frac{1}{12}$|+…+|$\frac{1}{49}$-$\frac{1}{50}$|
14．计算：
（1）|$\sqrt{3}$-4|-22+$\sqrt{12}$
（2）$\sqrt{32}$-$\sqrt{8}$+（$\sqrt{2}$-1）0+2$\sqrt{\frac{1}{2}}$．
4．若（m-7）m=1，则m=0，6，8．
11．太阳的半径约为696000000米，用科学记数法表示为6.96×108米．
8．在数轴上表示下列各数：0，-2.5，3$\frac{1}{2}$，-1，+6，-3．再按照从小到大的顺序用“＜”连接起来．
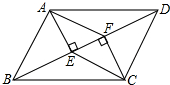9．如图，在?ABCD中，BD是对角线，AE⊥BD于点E，CF⊥BD于点F，试判断
（1）△ABE和△CDF全等吗？请说明理由；
（2）四边形AECF是不是平行四边形，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网