题目内容
20.在-$\frac{π}{3}$,3.1415,0,-0.333…,-$\frac{22}{7}$,-0.$\stackrel{•}{1}$$\stackrel{•}{5}$,2.010010001…中,有理数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解答 解:在-$\frac{π}{3}$,3.1415,0,-0.333…,-$\frac{22}{7}$,-0.$\stackrel{•}{1}$$\stackrel{•}{5}$,2.010010001…中,有理数有3.1415,0,-0.333…,-$\frac{22}{7}$,-0.$\stackrel{•}{1}$$\stackrel{•}{5}$,共有5个.
故选:D.
点评 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
15.多项式x2+3kxy-y2-9xy+10中,不含xy项,则k=( )
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
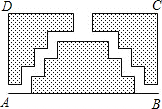 如图是一块长方形ABCD的场地,长AB=(3a+2)米,宽AD为(a+1)米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为3a2 平方米.
如图是一块长方形ABCD的场地,长AB=(3a+2)米,宽AD为(a+1)米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为3a2 平方米. 在数轴上表示下列各数:0,-2.5,3$\frac{1}{2}$,-1,+6,-3.再按照从小到大的顺序用“<”连接起来.
在数轴上表示下列各数:0,-2.5,3$\frac{1}{2}$,-1,+6,-3.再按照从小到大的顺序用“<”连接起来.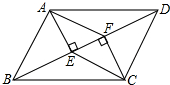 如图,在?ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断
如图,在?ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断