题目内容
16.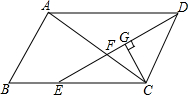 如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}$$\sqrt{3}$cm,则EF的长为$\sqrt{3}$cm.
如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}$$\sqrt{3}$cm,则EF的长为$\sqrt{3}$cm.
分析 利用平行四边形的性质以及角平分线的性质得出∠CDE=∠CED,进而求出DE的长,再利用相似三角形的判定与性质得出EF的长.
解答  解:∵在?ABCD中,∠ADC的平分线DE交BC于点E,
解:∵在?ABCD中,∠ADC的平分线DE交BC于点E,
∴∠ADE=∠EDC,∠ADE=∠DEC,AB=DC,
∴∠CDE=∠CED,
∵AB=3cm,AD=6cm,
∴DC=EC=3cm,
∵CG⊥DE,DG=$\frac{3}{2}$$\sqrt{3}$cm,
∴EG=$\frac{3}{2}$$\sqrt{3}$cm,
∴DE=3$\sqrt{3}$cm,
∵AD∥BC,
∴△AFD∽△CFE,
∴$\frac{AD}{EC}$=$\frac{DF}{EF}$,则$\frac{6}{3}$=$\frac{3\sqrt{3}-EF}{EF}$,
解得:EF=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识,得出△AFD∽△CFE是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列计算中,正确的是( )
| A. | 3-2=$\frac{1}{9}$ | B. | $\sqrt{(-3)^{2}}$=-3 | C. | m6÷m2=m3 | D. | (a-b)2=a2-b2 |
8.某服装店进购某种上衣和T恤衫共30件,进价和售价如表,全部销售完后,共获利润520元.
(1)求购进上衣,T恤衫各多少件?
(2)销售8件T恤衫的利润与销售几件上衣的利润相等?
| 上衣 | T恤衫 | |
| 进价(元/件) | 80 | 50 |
| 售价(元/件) | 100 | 65 |
(2)销售8件T恤衫的利润与销售几件上衣的利润相等?
14.$\sqrt{x-4}$有意义,x的取值范围是( )
| A. | x≠4 | B. | x≥4 | C. | x<4 | D. | x>4 |

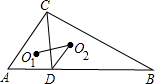 如图,△ABC中,CD⊥AB于D,O1、O2分别为△ACD和△BCD的内心,若AD=6,CD=8,BD=15,则cos∠O1O2D的值为$\frac{3\sqrt{13}}{13}$.
如图,△ABC中,CD⊥AB于D,O1、O2分别为△ACD和△BCD的内心,若AD=6,CD=8,BD=15,则cos∠O1O2D的值为$\frac{3\sqrt{13}}{13}$.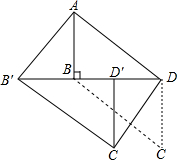 如图,在?ABCD中,AB⊥BD,AB=6,AD=3$\sqrt{13}$,将△BCD沿DB方向移动t个单位,得到△B′C′D′,连接AB′,C′D.
如图,在?ABCD中,AB⊥BD,AB=6,AD=3$\sqrt{13}$,将△BCD沿DB方向移动t个单位,得到△B′C′D′,连接AB′,C′D.