题目内容
11．
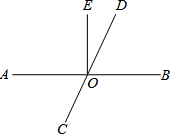如图所示，直线AB与直线CD相交于点O，EO⊥AB，∠EOD=25°，则∠AOC=65°，∠BOC=115°．
分析 首先根据邻补角的性质：邻补角互补，即和为180°，求出∠EOC的大小，再用它减去90°，求出∠AOC的大小；然后根据∠AOC和∠BOC是邻补角，用180°减去∠AOC的大小，求出∠BOC的大小即可．
解答 解：∵EO⊥AB，
∴∠AOE=90°，
∴∠AOC=180°-25°-90°
=155°-90°
=65°，
∴∠BOC=180°-∠AOC
=180°-65°
=115°
故答案为：65°．、115°．
点评 此题主要考查了垂线的性质和应用，以及邻补角的性质和应用，解答此题的关键是要明确邻补角的性质：邻补角互补，即和为180°．
练习册系列答案
相关题目
2．命题：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对顶角；④同位角相等．其中假命题有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
19．实数-27的立方根为（ ）
| A． | ±3 | B． | 3 | C． | -3 | D． | 没有立方根 |
16．
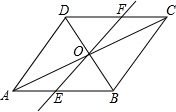如图，在平行四边形ABCD中，对角线AC，BD并于点O，经过点O的直线交AB于E，交CD于F．
①求证：OE=OF．
②连接DE，BF，则EF与BD满足什么条件时，四边形DEBF是矩形？请说明理由．
如图，在平行四边形ABCD中，对角线AC，BD并于点O，经过点O的直线交AB于E，交CD于F．①求证：OE=OF．
②连接DE，BF，则EF与BD满足什么条件时，四边形DEBF是矩形？请说明理由．
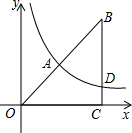如图，平面直角坐标系中，点B在第一象限，OC=BC，∠OCB=90°，OB=4$\sqrt{2}$，且反比例函数y=$\frac{m}{x}$（m≠0）的图象经过OB的中点A．
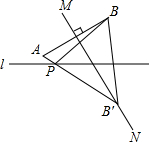如图，已知点B关于直线l的对称点是B′，AB的垂直平分线MN交BB′于B′，AB′交直线l于点P，点B到直线l的距离为3cm，求PA+PB的值．
1．把$\sqrt{\frac{8}{9}}$化为最简二次根式是（ ）
| A． | $\frac{\sqrt{8}}{3}$ | B． | $\frac{{2\sqrt{2}}}{{\sqrt{9}}}$ | C． | $\frac{2}{3}$ | D． | $\frac{2\sqrt{2}}{3}$ |