题目内容
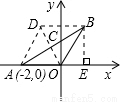
如图,OA=OB,点A的坐标是(-2,0),OB与x轴正方向夹角为600, 请画出过A,O,B三点的圆,写出圆心的坐标是 .
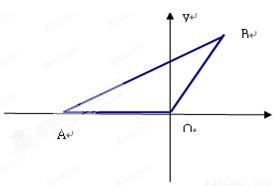
【解析】
如图;过B作BE⊥x轴于E;Rt△OBE中,OB=OA=2,∠BOE=60°;则OE=1,BE=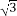 , 故B(1,
, 故B(1,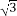 );以OA、OB为边作平行四边形AOBD,由于OA=OB,则四边形AOBD是菱形;所以点D一定在AB的垂直平分线上(菱形的对角线互相垂直平分);连接OA;由于OA=OD,∠DAO=∠BOE=60°,则△AOD是等边三角形;所以点D也在AO的垂直平分线上;故点D为△OAB的外心,所以D的坐标为(-1,
);以OA、OB为边作平行四边形AOBD,由于OA=OB,则四边形AOBD是菱形;所以点D一定在AB的垂直平分线上(菱形的对角线互相垂直平分);连接OA;由于OA=OD,∠DAO=∠BOE=60°,则△AOD是等边三角形;所以点D也在AO的垂直平分线上;故点D为△OAB的外心,所以D的坐标为(-1,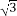 )
)
【解析】
试题分析:以OA、OB为边,AB为对角线作平行四边形AOBD,由于OA=OB,那么四边形AOBD是菱
形;由于菱形的对角线互相垂直平分,那么D点一定在AB的垂直平分线上;连接OD,易证得∠
DAO=60°,且AD=OA,所以点D也在OA的垂直平分线上;那么点D即为△AOB的外心,先求出B
点坐标,即可根据A、O、B三点坐标得到点D的坐标.
考点:三角形的外接圆与外心,坐标与图形的性质

练习册系列答案
相关题目
对于抛物线  .
.
(1)它与x轴交点的坐标为 ,与y轴交点的坐标为 ,顶点坐标为 ;
(2)在坐标系中利用描点法画出此抛物线;

x | … | … | |||||
y | … | … |
(3)利用以上信息解答下列问题:若关于x的一元二次方程 (t为实数)在
(t为实数)在 <x<
<x< 的范围内有解,则t的取值范围是 .
的范围内有解,则t的取值范围是 .
 的值.
的值.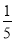 B.
B. C.
C. D.
D.
 知抛物线
知抛物线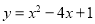 .
.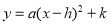 的形式;
的形式;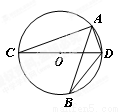
 在反比例函数
在反比例函数 的图象上,
的图象上, 轴于点
轴于点 ,
, 的面积为3,则
的面积为3,则 .
. 且
且 试化简:(1)
试化简:(1) (2)
(2)