题目内容
1.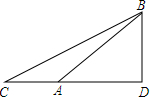 某商场准备改善原有楼梯的安全性能,把倾斜角由原来的40°减至35°.已知原楼梯AB的长为5m,调整后的楼梯所占地面CD有多长?(结果精确到0.1m)
某商场准备改善原有楼梯的安全性能,把倾斜角由原来的40°减至35°.已知原楼梯AB的长为5m,调整后的楼梯所占地面CD有多长?(结果精确到0.1m)(sin40°≈0.64,cos40°≈0.77,sin35°≈0.57,tan35°≈0.70)
分析 根据原楼梯的倾斜角为40°,可先求出AD的长,继而在Rt△ACD中求出CD的长.
解答 解:在Rt△ABD中,sin40°=$\frac{AD}{AB}$=$\frac{AD}{5}$,
∴AD=5sin40°=5×0.64=3.2,
在Rt△ACD中,tan35°=$\frac{AD}{CD}$,
CD=$\frac{3.2}{tan35°}$=4.6,
答:调整后的楼梯所占地面CD约为4.6米.
点评 本题考查了解直角三角形的实际应用中的坡度坡角问题,难度不大,注意细心运算即可

练习册系列答案
相关题目
9.当$\sqrt{x}+\sqrt{y}=\sqrt{5}-\sqrt{3},\sqrt{xy}=\sqrt{15}-\sqrt{3}$时,x+y的值为( )
| A. | 2 | B. | 5 | C. | $8-2\sqrt{15}$ | D. | $8-4\sqrt{15}+2\sqrt{3}$ |
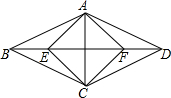 如图,菱形ABCD中,点E、F在对角线BD上,BE=DF=$\frac{1}{4}$BD,若四边形AECF为正方形,则tan∠ABE=$\frac{1}{2}$.
如图,菱形ABCD中,点E、F在对角线BD上,BE=DF=$\frac{1}{4}$BD,若四边形AECF为正方形,则tan∠ABE=$\frac{1}{2}$.