题目内容
13. 如图,△ABC中,若DE∥AC,$\frac{BD}{AB}$=$\frac{1}{3}$,DE=4cm,则AC的长为12 cm.
如图,△ABC中,若DE∥AC,$\frac{BD}{AB}$=$\frac{1}{3}$,DE=4cm,则AC的长为12 cm.
分析 由DE∥BC,即可得△BDE∽△BAC,又由相似三角形的对应边成比例,即可求得AC的长.
解答 解:∵DE∥AC,
∴△BDE∽△BAC,
∴$\frac{BD}{BA}=\frac{DE}{AC}$,
∵$\frac{BD}{AB}$=$\frac{1}{3}$,DE=4cm,
∴$\frac{1}{3}=\frac{4}{AC}$,
∴AC=12,
故答案为:12.
点评 此题考查了相似三角形的判定与性质.注意掌握数形结合思想的应用.

练习册系列答案
相关题目
4.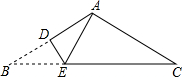 如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=6,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )
如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=6,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )
 如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=6,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )
如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=6,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )| A. | 1 | B. | 2 | C. | $2\sqrt{3}$ | D. | 3 |
5.若(a-2)2+|b+3|=0,则(a+b)2016的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2014 |
2.下列说法正确的是( )
| A. | 0是最小的整数 | |
| B. | 若|a|=|b|,则a=b | |
| C. | 互为相反数的两数之和为零 | |
| D. | 数轴上两个有理数,较大的数离原点较远 |
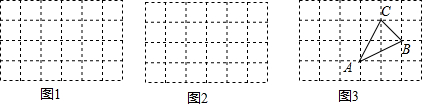 如图网格图中,每个小正方形的边长均为1,每个小格的顶点叫做格点.
如图网格图中,每个小正方形的边长均为1,每个小格的顶点叫做格点.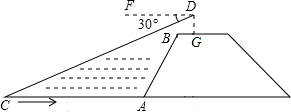 如图,小黄站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角是∠FDC=30°,若小黄的眼睛与地面的距离DG是1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡AB的坡度为i=4:3,坡长AB=10.5米,则此时小船C到岸边的距离CA的长为( )米.($\sqrt{3}$≈1.7,结果保留两位有效数字)
如图,小黄站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角是∠FDC=30°,若小黄的眼睛与地面的距离DG是1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡AB的坡度为i=4:3,坡长AB=10.5米,则此时小船C到岸边的距离CA的长为( )米.($\sqrt{3}$≈1.7,结果保留两位有效数字)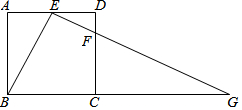 如图,在正方形中,点E是AD的中点,CF=3DF,连结并延长EF交BG的延长线于点G
如图,在正方形中,点E是AD的中点,CF=3DF,连结并延长EF交BG的延长线于点G