Question

3．已知等腰三角形△ABC，AB=AC，一腰上的中线把这个三角形的周长分成12和15两部分，则这个三角形的三边长分别为10，10，7或8，8，11．

Answer 1

分析 如图，在△ABC中，AB=AC，且AD=BD．设AB=x，BC=y，根据题意列方程即可得到结论．

解答 解：如图，在△ABC中，AB=AC，且AD=BD．设AB=x，BC=y，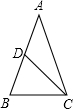
（1）当AC+AD=15，BD+BC=12时，则$\frac{x}{2}$+x=15，$\frac{x}{2}$+y=12，解得x=10，y=7．
（2）当AC+AD=12，BC+BD=15时，
则$\frac{x}{2}$+x=12，$\frac{x}{2}$+y=15，解得x=8，y=11，
故得这个三角形的三边长分别为10，10，7或8，8，11．
故答案为：10，10，7或8，8，11．

点评 本题考查了等腰三角形的性质，熟练掌握等腰三角形的性质是解题的关键．