Question

16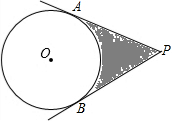．如图，PA，PB切⊙O于两点，若∠APB=60°，⊙O的半径为6，则阴影部分的面积为36$\sqrt{3}$-12π．

Answer 1

分析 连接OA、OB，连接OP，如图，根据切线的性质得OA⊥PA，OB⊥PB，根据切线长定理得PA=PB，∠OPA=∠OPB=$\frac{1}{2}$∠APB=30°，再利用四边形内角和得到∠AOB=180°-∠P=120°，接着在Rt△PAO中，根据含30度的直角三角形三边的关系计算出PA=$\sqrt{3}$OA=6 $\sqrt{3}$，利用三角形模糊公式可计算出S_{四边形AOBP}=2S_△OAP=36 $\sqrt{3}$，然后利用扇形的面积公式和阴影部分的面积=S_{四边形AOBP}-S_扇形AOB进行计算．

解答 解：连接OA、OB，连接OP，如图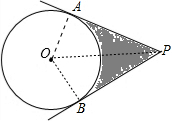
∵PA，PB分别切⊙O于点A、B，
∴OA⊥PA，OB⊥PB，PA=PB，∠OPA=∠OPB=$\frac{1}{2}$∠APB=30°，
∴∠OAP=∠OBP=90°，
而∠P=60°，
∴∠AOB=180°-∠P=120°，
在Rt△PAO中，∵OA=6，
∴PA=$\sqrt{3}$OA=6 $\sqrt{3}$，
∴S_{四边形AOBP}=2S_△OAP=2•$\frac{1}{2}$•6•6 $\sqrt{3}$=36 $\sqrt{3}$，
∴阴影部分的面积=S_{四边形AOBP}-S_扇形AOB=36 $\sqrt{3}$-$\frac{120•π•{6}^{2}}{360}$=36 $\sqrt{3}$-12π．
故答案为36 $\sqrt{3}$-12π．

点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了切线长定理和扇形的面积公式．