题目内容
3.已知方程x2-5x+1=0,求:(1)x+$\frac{1}{x}$的值;
(2)x2+$\frac{1}{{x}^{2}}$的值;
(3)x-$\frac{1}{x}$的值.
分析 (1)在已知方程的两边同时除以x,然后来求x+$\frac{1}{x}$的值;
(2)通过求(x+$\frac{1}{x}$)2来求x2+$\frac{1}{{x}^{2}}$的值;
(3)利用完全平方公式的变形公式进行解答.
解答 解:(1)在x2-5x+1=0的两边同时除以x,得x-5+$\frac{1}{x}$=0,
所以x+$\frac{1}{x}$=5;
(2)x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2=52-2=23;
(3)(x-$\frac{1}{x}$)2=(x+$\frac{1}{x}$)2-4=25-4=21,
所以x-$\frac{1}{x}$=±$\sqrt{21}$.
点评 本题考查了一元二次方程的解.找出x+$\frac{1}{x}$、x2+$\frac{1}{{x}^{2}}$、x-$\frac{1}{x}$间的关系是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
13.如果a>b,下列各式中不正确的是( )
| A. | a-4>b-4 | B. | -$\frac{a}{3}$<-$\frac{b}{3}$ | C. | -2a<-2b | D. | -5+a<-5+b |
19.下列各点中在函数y=2x-1的图象上的点是( )
| A. | (-1,2) | B. | (1,3) | C. | (2,3) | D. | (2,1) |
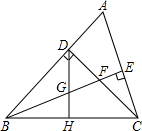 已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.