题目内容
已知,直线y=-| 2 | 3 |
 内作等腰Rt△ABC,∠BAC=90°.且点P(1,a)为坐标系中的一个动点.
内作等腰Rt△ABC,∠BAC=90°.且点P(1,a)为坐标系中的一个动点.(1)求三角形ABC的面积S△ABC;
(2)请说明不论a取任何实数,三角形BOP的面积是一个常数;
(3)要使得△ABC和△ABP的面积相等,求实数a的值.
分析:(1)先求出A、B两点的坐标,利用勾股定理得到AB的长,等腰Rt△ABC的面积为AB平方的一半;
(2)三角形BOP的底边BO=2,BO边上的高为P点的横坐标1,所以它的面积是一个常数1;
(3)实际上给定△ABP的面积,求P点坐标.利用面积和差求△ABP的面积,注意要分类讨论.
(2)三角形BOP的底边BO=2,BO边上的高为P点的横坐标1,所以它的面积是一个常数1;
(3)实际上给定△ABP的面积,求P点坐标.利用面积和差求△ABP的面积,注意要分类讨论.
解答:解:(1)令y=-
x+2中x=0,得点B坐标为(0,2);
令y=0,得点A坐标为(3,0).
由勾股定理可得|AB| =
,
所以S△ABC=6.5;
(2)不论a取任何实数,三角形BOP都可以以BO=2为底,点P到y轴的距离1为高,
所以S△BOP=1为常数;
(3)当点P在第四象限时,
因为S△ABO=3, S△APO=-
a,S△BOP=1,
所以S△ABP=S△ABO+S△APO-S△BOP=S△ABC=
,
即3-
a-1=
,解得a=-3,
当点P在第一象限时,
∵S△ABO=3,S△APO=
a,S△BOP=1,
∴S△ABP=S△BOP+S△AOP-S△ABO=
,
即1+
a-3=
,
用类似的方法可解得a=
.
| 2 |
| 3 |
令y=0,得点A坐标为(3,0).
由勾股定理可得|AB| =
| 13 |
所以S△ABC=6.5;
(2)不论a取任何实数,三角形BOP都可以以BO=2为底,点P到y轴的距离1为高,
所以S△BOP=1为常数;
(3)当点P在第四象限时,

因为S△ABO=3, S△APO=-
| 3 |
| 2 |
所以S△ABP=S△ABO+S△APO-S△BOP=S△ABC=
| 13 |
| 2 |
即3-
| 3 |
| 2 |
| 13 |
| 2 |
当点P在第一象限时,
∵S△ABO=3,S△APO=
| 3 |
| 2 |
∴S△ABP=S△BOP+S△AOP-S△ABO=
| 13 |
| 2 |
即1+
| 3 |
| 2 |
| 13 |
| 2 |
用类似的方法可解得a=
| 17 |
| 3 |
点评:掌握一次函数的性质,会求一次函数与两坐标轴的交点坐标;会用坐标表示线段;掌握用面积的和差表示不规则图形的面积.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
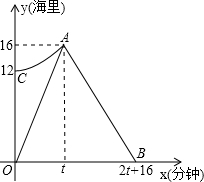 (2013•连云港)我市某海域内有一艘轮船发生故障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障渔船会合后立即将其拖回.如图折线段O-A-B表示救援船在整个航行过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律.抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律.已知救援船返程速度是前往速度的
(2013•连云港)我市某海域内有一艘轮船发生故障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障渔船会合后立即将其拖回.如图折线段O-A-B表示救援船在整个航行过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律.抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律.已知救援船返程速度是前往速度的
