��Ŀ����
��ֱ֪��l1��y=| 3 |
| 3 |
| 3 |
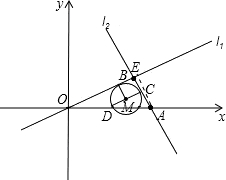
��1����A������ꣻ
��2����C���߶�AB�ϣ���C����CD��OB����x����D�㣬��֪���߶�CDΪֱ���ġ�M��ֱ��l1���У�
�����M�İ뾶r��
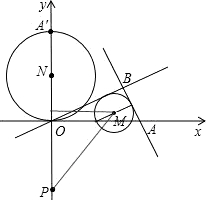
�����ѡ�OAB����ԭ��O��ʱ����ת90��õ���OA'B'����y�����Ƿ����һ��P��ʹ�á�P���M����OA'Ϊֱ���ġ�N�����У������ڣ������P������ꣻ�������ڣ���˵�����ɣ�
����������������ֱ���ཻ�ڵ�B�����bֵ�����������A�����꣮��2������Ҫ�������⻭��ͼ�Σ�����ֱ����Բ�ļ���λ�ù�ϵ�г���ϵʽ��⣮
��� �⣺��1���������֪��
�⣺��1���������֪��
y=-2��2+
����2
+b��
��ã�b=8+4
��
��ֱ��l2��y=-��2+
��x+8+4
��
��y=0�ã�0=-��2+
��x+8+4
�����x=4��
��A��4��0����
��2�������M��ֱ��l1�ľ���Ϊd������A��AE��l1�ڵ�E��
��Rt��AOE��AE=
��OA=2��
��CD��l1��
��
=
��
��d=2-r��
��OM��l1����
��2-r=r����r=1��
���������M��2+
��
����
���P�İ뾶ΪR��
������Բ���е����ʿɵã�
��һ������P���M����N������ʱ���ã�
��R+1��2=��2+
��2+��R+
��2�����R=4+2
��
��P1��0��-4-2
����
����������N����M�����P����ʱ���ã�
��R-1��2=��2+
��2+��R-
��2��
���R=
+
��4
��P2��0��
-
����
��������������������P�������ΪP1��0��-4-2
����P2��0��
-
����
 �⣺��1���������֪��
�⣺��1���������֪��y=-2��2+
| 3 |
| 3 |
��ã�b=8+4
| 3 |
��ֱ��l2��y=-��2+
| 3 |
| 3 |
��y=0�ã�0=-��2+
| 3 |
| 3 |
��A��4��0����
��2�������M��ֱ��l1�ľ���Ϊd������A��AE��l1�ڵ�E��
��Rt��AOE��AE=
| 1 |
| 2 |
��CD��l1��
��
| 2-d |
| 2 |
| 2r |
| 4 |
��d=2-r��
��OM��l1����
��2-r=r����r=1��
���������M��2+
| ||
| 2 |
| 1 |
| 2 |
���P�İ뾶ΪR��
������Բ���е����ʿɵã�
��һ������P���M����N������ʱ���ã�
��R+1��2=��2+
| ||
| 2 |
| 1 |
| 2 |
| 3 |

��P1��0��-4-2
| 3 |
����������N����M�����P����ʱ���ã�
��R-1��2=��2+
| ||
| 2 |
| 1 |
| 2 |
���R=
| 16 |
| 5 |
| 2 |
| 5 |
| 3 |
��P2��0��
| 4 |
| 5 |
| 2 |
| 5 |
| 3 |
��������������������P�������ΪP1��0��-4-2
| 3 |
| 4 |
| 5 |
| 2 |
| 5 |
| 3 |
�����������ۺϿ�����һ�κ����뼸��֪ʶ��Ӧ�ã���������Բ��ֱ�ߵĹ�ϵ�Լ�ֱ�������ε�֪ʶ����߶εij��ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����ֱ֪��l1��y=2x+3��ֱ��l2��y=-x+5��ֱ��l1��l2�ֱ�x����B��C���㣬l1��l2�ཻ�ڵ�A��
��ͼ����ֱ֪��l1��y=2x+3��ֱ��l2��y=-x+5��ֱ��l1��l2�ֱ�x����B��C���㣬l1��l2�ཻ�ڵ�A�� ��2013•���ϣ���ֱ֪��l1��l2��l3��l4�����ڵ�����ƽ��ֱ��ľ����Ϊh������ABCD���ĸ�����ֱ���������ֱ���ϣ����÷�ʽ��ͼ��ʾ��AB=4��BC=6����tan����ֵ���ڣ�������
��2013•���ϣ���ֱ֪��l1��l2��l3��l4�����ڵ�����ƽ��ֱ��ľ����Ϊh������ABCD���ĸ�����ֱ���������ֱ���ϣ����÷�ʽ��ͼ��ʾ��AB=4��BC=6����tan����ֵ���ڣ�������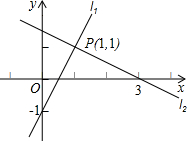 �����ṩ����Ϣ�ش��������⣺
�����ṩ����Ϣ�ش��������⣺ ��ͼ����ֱ֪��l1��l2�͡�ABC����l1��l2�ڵ�O����A��l1�ϣ���B����C��l2�ϣ�
��ͼ����ֱ֪��l1��l2�͡�ABC����l1��l2�ڵ�O����A��l1�ϣ���B����C��l2�ϣ� �Ķ�����IJ��ϣ�
�Ķ�����IJ��ϣ�