题目内容
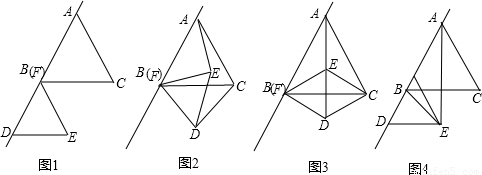
如图1,正△ABC和正△FDE,F与B重合,AB与FD在一条直线上.(1)若将△FDE绕点B旋转一定角度(如图2),试说明CD=AE;
(2)已知AB=6,DE=2
| 3 |
(3)若把图1中的正△FDE沿BA方向平移(如图4),连接AE、BE,已知正△ABC和正△FDE的边长分别是5cm和2
| 3 |
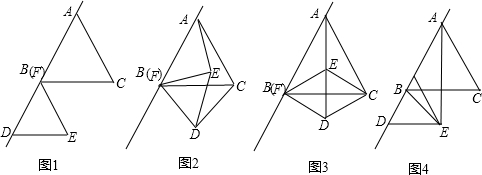
分析:(1)利用“SAS”证明AE、CD所在的三角形△ABE≌△CBD即可;
(2)设DE,BC交于O点,△FDE绕点B逆时针方向旋转90°时,∠DBA=90°,又∠CBA=60°,则∠DBC=30°=∠EBC,由等边三角形的性质可知BC垂直平分DE,解直角三角形求BO,证明DE垂直平分BC即可;
(3)会.根据运动过程中,△ABE为等腰三角形时,分AB=BE,BE=AE,AE=AB三种情况分别求解.
(2)设DE,BC交于O点,△FDE绕点B逆时针方向旋转90°时,∠DBA=90°,又∠CBA=60°,则∠DBC=30°=∠EBC,由等边三角形的性质可知BC垂直平分DE,解直角三角形求BO,证明DE垂直平分BC即可;
(3)会.根据运动过程中,△ABE为等腰三角形时,分AB=BE,BE=AE,AE=AB三种情况分别求解.
解答:证明:(1)如图2,
∵AB=BC,∠ABE=∠ABC-∠EBC=60°-∠EBC=∠CBD,BE=BD,
∴△ABE≌△CBD,
∴CD=AE;
解:(2)四边形EBDC为菱形.
理由:如图3,设DE,BC交于O点,
∵△FDE绕点B逆时针方向旋转90°时,∠DBA=90°,又∠CBA=60°,
∴∠DBC=30°=∠EBC,∴BC垂直平分DE,
在Rt△DBO中,BO=BD•cos30°=2
×
=3=
AB,
∴DE垂直平分BC,
对角线互相垂直平分的四边形为菱形,
∴四边形EBDC为菱形;
(3)△ABE会成为等腰三角形,此时FB=1+
或2.5+
或9+
或4+
.
∵AB=BC,∠ABE=∠ABC-∠EBC=60°-∠EBC=∠CBD,BE=BD,
∴△ABE≌△CBD,
∴CD=AE;
解:(2)四边形EBDC为菱形.
理由:如图3,设DE,BC交于O点,
∵△FDE绕点B逆时针方向旋转90°时,∠DBA=90°,又∠CBA=60°,
∴∠DBC=30°=∠EBC,∴BC垂直平分DE,
在Rt△DBO中,BO=BD•cos30°=2
| 3 |
| ||
| 2 |
| 1 |
| 2 |
∴DE垂直平分BC,
对角线互相垂直平分的四边形为菱形,
∴四边形EBDC为菱形;
(3)△ABE会成为等腰三角形,此时FB=1+
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查了菱形的性质,旋转、平移的性质.关键是根据两个等边三角形的特殊性,证明全等三角形,解直角三角形.

练习册系列答案
相关题目
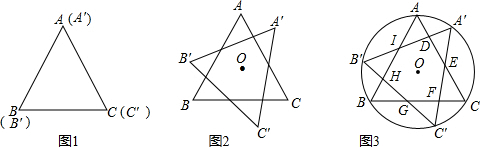
 ,把图1中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;
,把图1中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;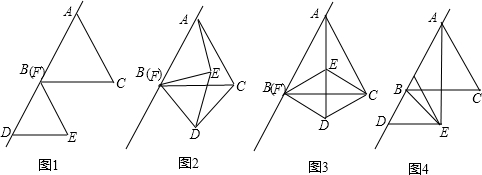

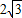 ,把图1中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;
,把图1中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;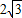 cm,问在平移过程中,△ABE是否会成为等腰三角形?若能,直接写出FB的值;若不能,说明理由.
cm,问在平移过程中,△ABE是否会成为等腰三角形?若能,直接写出FB的值;若不能,说明理由.