题目内容
11.某宾馆准备购进一批换气扇,从电器商场了解到:一台A型换气扇和三台B型换气扇共需275元;三台A型换气扇和二台B型换气扇共需300元.(1)求一台A型换气扇和一台B型换气扇的售价各是多少元;
(2)若该宾馆准备同时购进这两种型号的换气扇共40台并且A型换气扇的数量不多于B型换气扇数量的3倍,请设计出最省钱的购买方案,并说明理由.
分析 (1)设一台A型换气扇x元,一台B型换气扇的售价为y元,根据“一台A型换气扇和三台B型换气扇共需275元;三台A型换气扇和二台B型换气扇共需300元”列方程组求解即可;
(2)首先确定自变量的取值范围,然后得到有关总费用和换气扇的台数之间的关系得到函数解析式,确定函数的最值即可;
解答 解:(1)设一台A型换气扇x元,一台B型换气扇的售价为y元,根据题意得:
$\left\{\begin{array}{l}{x+3y=275}\\{3x+2y=300}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=50}\\{y=75}\end{array}\right.$,
答:一台A型换气扇50元,一台B型换气扇的售价为75元;
(2)设购进A型换气扇z台,总费用为w元,
则有z≤3(40-z),
解得:z≤30,
∵z为换气扇的台数,
∴z≤30且z为正整数,
w=50z+75(40-z)=-25z+3000,
∵-25<0,
∴w随着z的增大而减小,
∴当z=30时,w最大=25×30+3000=2250,
此时40-z=40-30=10,
答:最省钱的方案是购进30台A型换气扇,10台B型换气扇.
点评 此题主要考查了二元一次方程组的应用以及一次函数的应用等知识,根据题意得出正确的等量关系是解题关键,难度不大.

练习册系列答案
相关题目
19.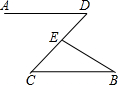 如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )
如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )
 如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )
如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )| A. | 72° | B. | 68° | C. | 63° | D. | 18° |
 已知数a与数b所表示的点在数轴上如图所示,则|a+b|-a=b.
已知数a与数b所表示的点在数轴上如图所示,则|a+b|-a=b. 胡老师散步途径A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东45°方向,在B地正北方向,在C地北偏西60°方向,C地在A地北偏东75°方向,B、D两地相距2km.问奥运圣火从A地传到D地的路程(即A→B→C→D的路程)大约是多少?(最后结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
胡老师散步途径A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东45°方向,在B地正北方向,在C地北偏西60°方向,C地在A地北偏东75°方向,B、D两地相距2km.问奥运圣火从A地传到D地的路程(即A→B→C→D的路程)大约是多少?(最后结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)