题目内容
9. 如图,A为双曲线y=$\frac{4}{x}$(x>0)上一点,B为x轴正半轴上一点,线段AB的中点C恰好在双曲线上,则△OAC的积为3.
如图,A为双曲线y=$\frac{4}{x}$(x>0)上一点,B为x轴正半轴上一点,线段AB的中点C恰好在双曲线上,则△OAC的积为3.
分析 作AD⊥x轴于D,CE⊥x轴于E,设A点坐标为(a,$\frac{4}{a}$),由于点C为AB的中点,则CE=$\frac{1}{2}$AD=$\frac{2}{a}$,DE=BE,根据反比例函数图象上点的坐标特征得到C点坐标为(2a,$\frac{2}{a}$),所以OD=DE=BE=a,根据反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义得到S△OAD=2,根据三角形面积公式得到S△AOB=3S△OAD=6,S△AOC=$\frac{1}{2}$S△OAB=3.
解答 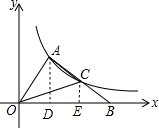 解:作AD⊥x轴于D,CE⊥x轴于E,如图,
解:作AD⊥x轴于D,CE⊥x轴于E,如图,
设A点坐标为(a,$\frac{4}{a}$),
∵点C为AB的中点,
∴CE=$\frac{1}{2}$AD=$\frac{2}{a}$,DE=BE,
∴C点坐标为(2a,$\frac{2}{a}$),
∴OD=DE=BE=a,
∵S△OAD=$\frac{1}{2}$×4=2,
∴S△AOB=3S△OAD=6,
∴S△AOC=$\frac{1}{2}$S△OAB=3.
故答案是:3.
点评 本题考查反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.本知识点是中考的重要考点,同学们应高度关注.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
20.下列计算正确的是( )
| A. | 2$\sqrt{\frac{1}{2}}$=$\sqrt{2}$ | B. | $\sqrt{2}$$+\sqrt{3}$=$\sqrt{5}$ | C. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | D. | 3+2$\sqrt{2}$=5$\sqrt{2}$ |
 若关于x的不等式组的解表示在数轴上如图所示,则这个不等式组的解1<x≤2.
若关于x的不等式组的解表示在数轴上如图所示,则这个不等式组的解1<x≤2.