题目内容
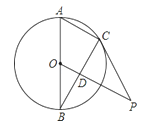
【题目】如图,![]() 是圆
是圆![]() 的直径,弦
的直径,弦![]() 于
于![]() ,
,![]() ,
,![]() ,则弦
,则弦![]() 的长为( )
的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
连接OC,由直径AB垂直于弦CD,利用垂径定理得到P为CD的中点,由CD的长求出CP的长,在直角三角形OCP中,由OP与PC的长,利用勾股定理求出OC的长,即为OA的长,由AO+OP求出AP的长,在直角三角形ACP中,由AP与PC的长,利用勾股定理即可求出AC的长.
连接OC,如图所示:

∵直径AB⊥CD,CD=2![]() ,
,
∴P为CD的中点,即CP=DP=![]() ,
,
在Rt△OCP中,OP=1,CP=![]() ,
,
根据勾股定理得:OC=![]() =2,
=2,
则OA=OC=2,
则AP=AO+OP=2+1=3,
在Rt△APC中,AP=3,CP=![]() ,
,
根据勾股定理得:AC=![]() =2
=2![]() .
.
故选:C.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目