题目内容
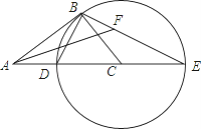
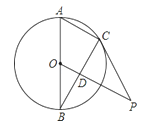
【题目】如图，AB为⊙O的直径，D为弦BC的中心，连接OD并延长交过点C的切线于点P，连接AC．求证：△CPD∽△ABC．
【答案】详见解析.
【解析】
连接OC．则∠OCP=90°，再由AB是⊙O的直径，得AC⊥CD．根据D为弦BC的中心，则OP⊥BC，再由弦切角定理得出∠PCD=∠A，从而得出结论．
证明：连接OC．
∵PC是⊙O的切线，点C为切点，
∴∠OCP=90°．
∵AB是⊙O的直径，
∴AC⊥CD．
又点D为弦BC的中点，
∴OP⊥CD．
∴∠P+∠POC=90°，
∠OCD+∠POC=90°．
∴∠P=∠OCD．
∵OC=OB，
∴∠OCD=∠B．
∴∠P=∠B．
∵AB是⊙O的直径，
∴∠ACB=90°．
∴∠CDP=∠ACB=90°．
∴△CDP∽△ABC．
练习册系列答案
相关题目
【题目】八（1）班五位同学参加学校举办的数学竞赛，试卷中共有20道题，规定每题答对得5分，答错扣2分，未答得0分。赛后A，B， C，D，E五位同学对照评分标准回忆并记录了自己的答题情况（E同学只记得有7道题未答），具体如下表：
参赛同学 | 答对题数 | 答错题数 | 未答题数 |
A | 19 | 0 | 1 |
B | 17 | 2 | 1 |
C | 15 | 2 | 3 |
D | 17 | 1 | 2 |
E | / | / | 7 |
（1）根据以上信息，求A，B，C，D四位同学成绩的平均分；
（2）最后获知：A，B，C，D，E五位同学成绩分别是95分，81分，64分，83分，58分.
①求E同学的答对题数和答错题数；
②经计算，A，B，C，D四位同学实际成绩平均分是80.75分，与（1）中算得的平均分不相符，发现是其中一位同学记错了自己的答题情况.请指出哪位同学记错了，并写出他的实际答题情况（直接写出答案即可）.
