��Ŀ����
11�����и�����ֵ�Ƿ���2x-y=3�Ľ���ǣ�������| A�� | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ |
���� ���ݷ��̵Ľ����㷽�̣��ɵô𰸣�
��� �⣺A��x=1��2-y=3�����y=-1����Ԫһ�η��̵Ľ���$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$����A����
B��x=2��4-y=3�����y=1����Ԫһ�η��̵Ľ���$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$����B��ȷ��
C��x=1��2-y=3�����y=-1����Ԫһ�η��̵Ľ���$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$����C����
D��x=2��4-y=3�����y=1����Ԫһ�η��̵Ľ���$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$����D����
��ѡ��B��
���� ���⿼���˶�Ԫһ�η��̵Ľ⣬ʹ��Ԫһ�η��̳�����δ֪����֪��������鷨�ǽ���ؼ���

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
1��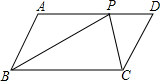 ��ͼ��ƽ���ı���ABCD�У�P�DZ�AD�ϼ�����һ�㣨����A��D�⣩����ABP����BCP����CDP������ֱ�ΪS1��S2��S3����һ���������ǣ�������
��ͼ��ƽ���ı���ABCD�У�P�DZ�AD�ϼ�����һ�㣨����A��D�⣩����ABP����BCP����CDP������ֱ�ΪS1��S2��S3����һ���������ǣ�������
 ��ͼ��ƽ���ı���ABCD�У�P�DZ�AD�ϼ�����һ�㣨����A��D�⣩����ABP����BCP����CDP������ֱ�ΪS1��S2��S3����һ���������ǣ�������
��ͼ��ƽ���ı���ABCD�У�P�DZ�AD�ϼ�����һ�㣨����A��D�⣩����ABP����BCP����CDP������ֱ�ΪS1��S2��S3����һ���������ǣ�������| A�� | S1+S3��S2 | B�� | S1+S3��S2 | C�� | S1+S3=S2 | D�� | S1+S2=S3 |
19����|x+y-1|+��y+3��2=0����$\frac{1}{4}$x-2y��ֵ�ǣ�������
| A�� | 1 | B�� | -1 | C�� | 7 | D�� | -7 |
3�����м��㣬��10=0 ��2-3=-8 ��a2n��a2n=a ��a+a2=a3 �ݣ�a+b��2=a2+b2��������У�������
| A�� | 5�� | B�� | 4�� | C�� | 3�� | D�� | 2�� |
 ����ͼ��ʾ��ֱ��������ֱ��l��תһ�ܣ��õ�������ͼ���ǣ�������
����ͼ��ʾ��ֱ��������ֱ��l��תһ�ܣ��õ�������ͼ���ǣ�������


