题目内容
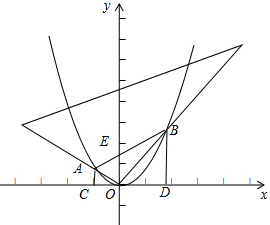 在坐标系中,有一直角三角尺的直角顶点与原点O重合,旋转它时与抛物线y=x2交于点A、B,分别过A、B作x轴的垂线交x轴于点C、D.
在坐标系中,有一直角三角尺的直角顶点与原点O重合,旋转它时与抛物线y=x2交于点A、B,分别过A、B作x轴的垂线交x轴于点C、D.(1)设A、B的横坐标分别为a、b,写出b与a之间的函数关系式;
(2)证明:AB必过y轴上一定点;
(3)设点E(x,y)是AB的中点,求y与x的关系式.
考点:二次函数综合题
专题:
分析:(1)运用抛物线求出点A、B的坐标.再运用正切求出ab=-1.
(2)设y=mx+n,利用点坐标求出直线解析式,x=0时,y=1.即得AB必过y轴上一定点(0,1);
(3)由点A、B的坐标.求出点E(x,y)是AB的中点,再由ab=-1.求出y与x的关系式.
(2)设y=mx+n,利用点坐标求出直线解析式,x=0时,y=1.即得AB必过y轴上一定点(0,1);
(3)由点A、B的坐标.求出点E(x,y)是AB的中点,再由ab=-1.求出y与x的关系式.
解答:(1)解:∵抛物线y=x2,A、B的横坐标分别为a、b,
∴A(a,a2),B(b,b2).
∵一直角三角尺的直角顶点与原点O重合,
∴tan∠AOC=tan∠OBD,即
=
,
=
,
∴ab=-1.
(2)证明:设y=mx+n
∵A(a,a2),B(b,b2).
∴
,
解得
,
∴y=(a+b)x-ab.
∴x=0时,y=1.
∴AB必过y轴上一定点(0,1);
(3)解:∵A(a,a2),B(b,b2).点E(x,y)是AB的中点,
∴x=
,y=
=
,
∴y=2x2+1.
∴A(a,a2),B(b,b2).
∵一直角三角尺的直角顶点与原点O重合,
∴tan∠AOC=tan∠OBD,即
| AC |
| CO |
| OD |
| BD |
| a2 |
| -a |
| b |
| b2 |
∴ab=-1.
(2)证明:设y=mx+n
∵A(a,a2),B(b,b2).
∴
|
解得
|
∴y=(a+b)x-ab.
∴x=0时,y=1.
∴AB必过y轴上一定点(0,1);
(3)解:∵A(a,a2),B(b,b2).点E(x,y)是AB的中点,
∴x=
| a+b |
| 2 |
| a2+b2 |
| 2 |
| (a+b)2-2ab |
| 2 |
∴y=2x2+1.
点评:本题主要考查了二次函数综合题,解题的关键是求出ab=-1.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 如图所示直线a和b,及点P和Q.试确定点M,使M到直线a和b的距离相等且到P和Q两点的距离也相等.
如图所示直线a和b,及点P和Q.试确定点M,使M到直线a和b的距离相等且到P和Q两点的距离也相等.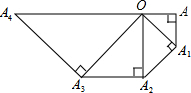 如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰
如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰 如图,点O为矩形ABCD的中心,AB=3,BC=4,过O、D两点的圆分别交矩形两边AD、DC于M、N.求MN的最小值.
如图,点O为矩形ABCD的中心,AB=3,BC=4,过O、D两点的圆分别交矩形两边AD、DC于M、N.求MN的最小值. 将图中的△ABC作下列运动,画出相应的图形,指出三个顶点的坐标所发生的变化.(网格可自行补充)
将图中的△ABC作下列运动,画出相应的图形,指出三个顶点的坐标所发生的变化.(网格可自行补充) 如图,将二次函数y=x2-3的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象,当直线y=x+b与此图象有两个公共点时,求b的取值范围
如图,将二次函数y=x2-3的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象,当直线y=x+b与此图象有两个公共点时,求b的取值范围 如图,BD=CD,请你增加一个条件
如图,BD=CD,请你增加一个条件