题目内容
 如图,将二次函数y=x2-3的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象,当直线y=x+b与此图象有两个公共点时,求b的取值范围
如图,将二次函数y=x2-3的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象,当直线y=x+b与此图象有两个公共点时,求b的取值范围考点:二次函数图象与几何变换
专题:数形结合
分析:分类讨论:当直线y=x+b与y=x2-3(x>
或x<-
)有两个公共点时,x2-x-3-b=0,利用判别式的意义得到b>
;根据图象,当直线y=x+b经过点(-
,0)与点(
,0)之间时,直线y=x+b与此图象有两个公共点时,把两点坐标代入y=x+b可得到b的范围.
| 3 |
| 3 |
| 13 |
| 4 |
| 3 |
| 3 |
解答:解:二次函数y=x2-3与x轴的交点坐标为(-
,0)、(
,0),
当直线y=x+b与y=x2-3(x>
或x<-
)有两个公共点时,x2-x-3-b=0,△=1-4(-3-b)>0,解得b>
;
当直线y=x+b经过点(-
,0)与点(
,0)之间时,直线y=x+b与此图象有两个公共点时,解得-
<b<
,
所以b的取值范围为b>
或-
<b<
.
故答案为b>
或-
<b<
.
| 3 |
| 3 |
当直线y=x+b与y=x2-3(x>
| 3 |
| 3 |
| 13 |
| 4 |
当直线y=x+b经过点(-
| 3 |
| 3 |
| 3 |
| 3 |
所以b的取值范围为b>
| 13 |
| 4 |
| 3 |
| 3 |
故答案为b>
| 13 |
| 4 |
| 3 |
| 3 |
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
过圆上一点可以作圆的最长弦有( )条.
| A、1 | B、2 | C、3 | D、无数条 |
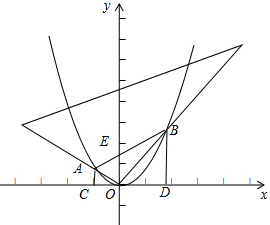 在坐标系中,有一直角三角尺的直角顶点与原点O重合,旋转它时与抛物线y=x2交于点A、B,分别过A、B作x轴的垂线交x轴于点C、D.
在坐标系中,有一直角三角尺的直角顶点与原点O重合,旋转它时与抛物线y=x2交于点A、B,分别过A、B作x轴的垂线交x轴于点C、D. 如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于F,EF⊥BD,求证:四边形EBFD是菱形.
如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于F,EF⊥BD,求证:四边形EBFD是菱形.