题目内容
 如图,点O为矩形ABCD的中心,AB=3,BC=4,过O、D两点的圆分别交矩形两边AD、DC于M、N.求MN的最小值.
如图,点O为矩形ABCD的中心,AB=3,BC=4,过O、D两点的圆分别交矩形两边AD、DC于M、N.求MN的最小值.考点:矩形的性质,圆周角定理
专题:
分析:根据题意得出过点O和D点的最小圆即DO为直径,进而利用勾股定理求出即可.
解答:解:∵∠D=90°,
∴MN是圆的直径,
∴所求为过点O和D点的最小圆,
∴以OD为直径的圆为所求,
∴MN=OD,
则BD=
=5,则OD=
,
故MN的最小值为:
.
∴MN是圆的直径,
∴所求为过点O和D点的最小圆,
∴以OD为直径的圆为所求,
∴MN=OD,
则BD=
| 32+42 |
| 5 |
| 2 |
故MN的最小值为:
| 5 |
| 2 |
点评:此题主要考查了矩形的性质以及勾股定理和圆周角定理等知识,得出以OD为直径的圆为所求是解题关键.

练习册系列答案
相关题目
过圆上一点可以作圆的最长弦有( )条.
| A、1 | B、2 | C、3 | D、无数条 |
 一个点从数轴原点开始,先向右移动3个单位长度,再向右移动2个单位长度,如图所示,由图可以看出,到达的终点是表示5的点.画图表示一个点在数轴上按如下方式移动达到的终点,并说明它表示的是什么数的点,从原点开始向右移动-4个单位长度,再向左移动-3个长度单位.
一个点从数轴原点开始,先向右移动3个单位长度,再向右移动2个单位长度,如图所示,由图可以看出,到达的终点是表示5的点.画图表示一个点在数轴上按如下方式移动达到的终点,并说明它表示的是什么数的点,从原点开始向右移动-4个单位长度,再向左移动-3个长度单位.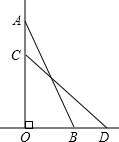 如图,一个25m长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24m,如果梯子的顶端A沿墙下滑4m,那么梯子底端B也外移4m吗?
如图,一个25m长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24m,如果梯子的顶端A沿墙下滑4m,那么梯子底端B也外移4m吗?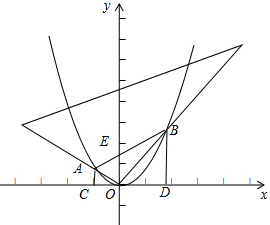 在坐标系中,有一直角三角尺的直角顶点与原点O重合,旋转它时与抛物线y=x2交于点A、B,分别过A、B作x轴的垂线交x轴于点C、D.
在坐标系中,有一直角三角尺的直角顶点与原点O重合,旋转它时与抛物线y=x2交于点A、B,分别过A、B作x轴的垂线交x轴于点C、D.