题目内容
5.阅读所给的材料,然后解答问题:如图①,在“格点”直角坐标系上我们可以发现:求线段DE的长度,可以转化为求Rt△DEF的斜边长,例如:在坐标系中我们发现:D(-7,5),E(4,-3),所以DF=|5-(-3)|=8,EF=|4-(-7)|=11,所以据勾股定理可得:DE=$\sqrt{{8}^{2}+1{1}^{2}}$=$\sqrt{185}$.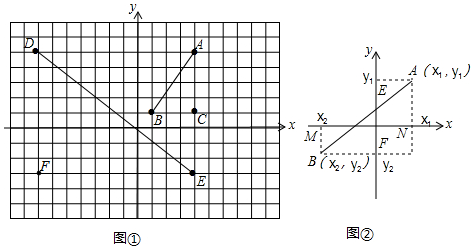
(1)在图①中用上面的方法可求出线段AB的长为5;
(2)在图②中:设A(x1.y1),B(x2,y2),试用x1,x2,y1,y2表示:AC=y1-y2,BC=x1-x2,AB$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$;
(3)已知A(2,1),B(4,3),试用(2)中得出的结论求线段AB的长;
(4)已知A(2,1),B(4,3),若点C为y轴上的点且使得△ABC是以AB为底边的等腰三角形,试求出点C的坐标.
分析 (1)根据图①确定出BC与AC的长,利用勾股定理求出AB的长即可;
(2)在图②中,由A与B的坐标表示出AC,BC,利用勾股定理表示出AB的长即可;
(3)利用题中的方法,根据A与B坐标求出AB的长即可;
(4)设C(0,y),由题意得到AC=BC,根据A与B坐标,利用题中的方法列出方程,求出方程的解得到y的值,即可确定出C坐标.
解答 解:(1)根据题意得:AB=$\sqrt{{3}^{2}+{4}^{2}}$=5;
(2)根据题意得:AC=y1-y2;BC=x1-x2,AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$;
(3)∵A(2,1),B(4,3),
∴AB=$\sqrt{(2-4)^{2}+(1-3)^{2}}$=2$\sqrt{2}$;
(4)设C坐标为(0,y),A(4,5),B(1,1),
根据题意得:AC=BC,即$\sqrt{(0-4)^{2}+(y-5)^{2}}$=$\sqrt{(0-1)^{2}+(y-1)^{2}}$,
解得:y=$\frac{39}{8}$,
则C坐标为(0,$\frac{39}{8}$).
故答案为:(1)5;(2)y1-y2;x1-x2,$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
点评 此题属于一次函数综合题,涉及的知识有:坐标与图形性质,弄清题中阅读材料中求两点间的距离公式是解本题的关键.

练习册系列答案
相关题目
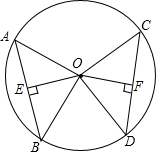 AB,CD是⊙O的两条弦,若OE⊥AB于点E,OF⊥CD于点F,且$\widehat{AB}$=$\widehat{CD}$,求证:OE=OF.
AB,CD是⊙O的两条弦,若OE⊥AB于点E,OF⊥CD于点F,且$\widehat{AB}$=$\widehat{CD}$,求证:OE=OF.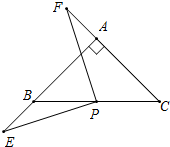 如图1,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、CA的延长线于点E、F.
如图1,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、CA的延长线于点E、F.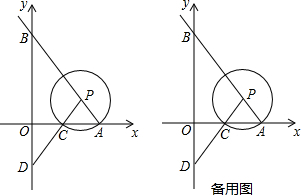 已知:平面直角坐标系中点A(3,0),B(0,4),点P是射线AB上一动点(点P与点A、B重合),设AP=r,以点P为圆心,r为半径作⊙P,⊙P的交x轴于一点C,直线PC交y轴于点D,点E是BD的中点,射线PE交⊙P于点F,连接OF.
已知:平面直角坐标系中点A(3,0),B(0,4),点P是射线AB上一动点(点P与点A、B重合),设AP=r,以点P为圆心,r为半径作⊙P,⊙P的交x轴于一点C,直线PC交y轴于点D,点E是BD的中点,射线PE交⊙P于点F,连接OF. 如图,在直角坐标系中,以点A($\sqrt{3}$,0)为圆心,以2$\sqrt{3}$为半径的圆与x轴交于B,C两点,与y轴交于D,E两点.
如图,在直角坐标系中,以点A($\sqrt{3}$,0)为圆心,以2$\sqrt{3}$为半径的圆与x轴交于B,C两点,与y轴交于D,E两点.