题目内容
13.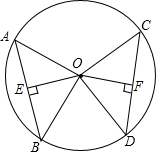 AB,CD是⊙O的两条弦,若OE⊥AB于点E,OF⊥CD于点F,且$\widehat{AB}$=$\widehat{CD}$,求证:OE=OF.
AB,CD是⊙O的两条弦,若OE⊥AB于点E,OF⊥CD于点F,且$\widehat{AB}$=$\widehat{CD}$,求证:OE=OF.
分析 如图,首先证明AE=CF(设为λ),证明OE=$\sqrt{{μ}^{2}-{λ}^{2}}$,OF=$\sqrt{{μ}^{2}-{λ}^{2}}$,即可解决问题.
解答  解:如图,∵$\widehat{AB}$=$\widehat{CD}$,
解:如图,∵$\widehat{AB}$=$\widehat{CD}$,
∴AB=CD;∵OE⊥AB,OF⊥CD,
∴AE=$\frac{1}{2}$AB,CF=$\frac{1}{2}$CD;
∴AE=CF(设为λ),设⊙O的半径为μ,
由勾股定理得:OE=$\sqrt{{μ}^{2}-{λ}^{2}}$,OF=$\sqrt{{μ}^{2}-{λ}^{2}}$,
∴OE=OF.
点评 该题主要考查了垂径定理、勾股定理等几何知识点及其应用问题;应牢固掌握垂径定理、勾股定理等几何知识点,这是灵活解题的基础和关键.

练习册系列答案
相关题目
4. 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④AB=HF,其中正确的有( )
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④AB=HF,其中正确的有( )
 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④AB=HF,其中正确的有( )
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④AB=HF,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
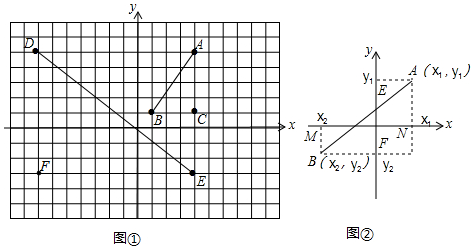
2.根据下列表述,能确定具体位置的是( )
| A. | 某电影院2排 | B. | 北京市东直门大街 | ||
| C. | 东经118°,北纬30° | D. | 北偏东60° |
 已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.
已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.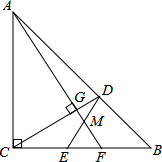 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E,F为线段BC上的两点,且CE=BF,连接AF,过点C作CD⊥AF于点G,交AB于点D,连接DE,交AF于点M.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E,F为线段BC上的两点,且CE=BF,连接AF,过点C作CD⊥AF于点G,交AB于点D,连接DE,交AF于点M.