题目内容
11.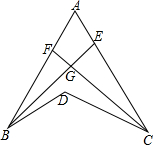 如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,则∠A为( )
如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,则∠A为( )| A. | 70° | B. | 75° | C. | 80° | D. | 85° |
分析 首先根据三角形的内角和定理,求出∠1+∠2=40°,∠1+∠2+∠3+∠4=70°;然后判断出∠3+∠4=30°,再根据BE是∠ABD的平分线,CF是∠ACD的平分线,判断出∠5+∠6=30°;最后根据三角形的内角和定理,用180°减去∠1+∠2+∠3+∠4+∠5+∠6的度数,求出∠A为多少度即可.
解答 解:如图,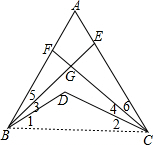 ,
,
∵∠BDC=140°,
∴∠1+∠2=180°-140°=40°,
∵∠BGC=110°,
∴∠1+∠2+∠3+∠4=180°-110°=70°,
∴∠3+∠4=70°-40°=30°,
∵BE是∠ABD的平分线,CF是∠ACD的平分线,
∴∠3=∠5,∠4=∠6,
又∵∠3+∠4=30°,
∴∠5+∠6=30°,
∴∠1+∠2+∠3+∠4+∠5+∠6
=(∠1+∠2+∠3+∠4)+(∠5+∠6)
=70°+30°
=100°
∴∠A=180°-100°=80°.
故选:C.
点评 (1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.
(2)此题还考查了角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:一个角的平分线把这个角分成两个大小相同的角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知9m=$\frac{2}{3}$,3n=$\frac{1}{2}$;则下列结论正确的是( )
| A. | 2m-n=$\frac{4}{3}$ | B. | 2m+n=-1 | C. | 2m-n=3 | D. | $\frac{2m}{n}$=3 |
19.已知$\left\{\begin{array}{l}a=2t+3\\ b=3t-1\end{array}\right.$,则用含a的代数式表示b,得( )
| A. | $b=\frac{3a-11}{2}$ | B. | b=3a-1 | C. | $b=\frac{3a-7}{3}$ | D. | $b=\frac{3a+1}{2}$ |
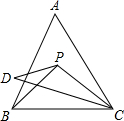 如图所示,P是等边△ABC内一点,PB=PC,∠PCD=∠PBA,且DC=BC,求∠D的度数.
如图所示,P是等边△ABC内一点,PB=PC,∠PCD=∠PBA,且DC=BC,求∠D的度数.