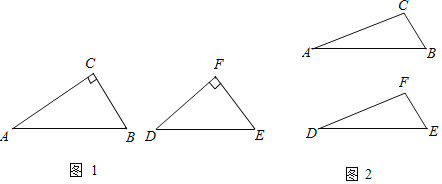Ő‚ńŅńŕ»›
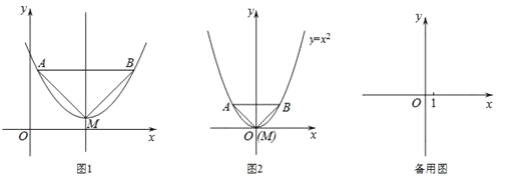
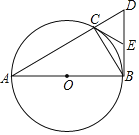
°ĺŐ‚ńŅ°Ņ»ÁÕľ£®1£©“—÷™ĺō–ő![]() ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ
‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() Ķ„Ķń◊ÝĪÍő™
Ķ„Ķń◊ÝĪÍő™![]() £¨∂ĮĶ„
£¨∂ĮĶ„![]() “‘√Ņ√Ž2łŲĶ•őĽ≥§∂»ĶńňŔ∂»—ō
“‘√Ņ√Ž2łŲĶ•őĽ≥§∂»ĶńňŔ∂»—ō![]() ‘ň∂Į£®
‘ň∂Į£®![]() Ķ„≤Ľ”ŽĶ„
Ķ„≤Ľ”ŽĶ„![]() °ĘĶ„
°ĘĶ„![]() ÷ōļŌ£©£¨…Ť‘ň∂Į Īľšő™
÷ōļŌ£©£¨…Ť‘ň∂Į Īľšő™![]() √Ž£ģ
√Ž£ģ
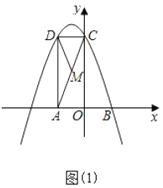
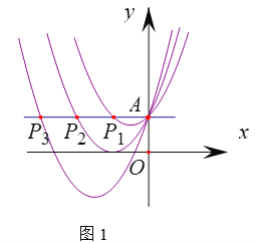
£®1£©«ůĺ≠Ļż![]() °Ę
°Ę![]() °Ę
°Ę![]() »żĶ„ĶńŇ◊őÔŌŖĹ‚őŲ Ĺ£Ľ
»żĶ„ĶńŇ◊őÔŌŖĹ‚őŲ Ĺ£Ľ
£®2£©Ķ„![]() ‘ŕ£®1£©÷–ĶńŇ◊őÔŌŖ…Ō£¨ĶĪ
‘ŕ£®1£©÷–ĶńŇ◊őÔŌŖ…Ō£¨ĶĪ![]() ő™
ő™![]() ÷–Ķ„ Ī£¨»Ű
÷–Ķ„ Ī£¨»Ű![]() £¨«ůĶ„
£¨«ůĶ„![]() Ķń◊ÝĪÍ£Ľ
Ķń◊ÝĪÍ£Ľ
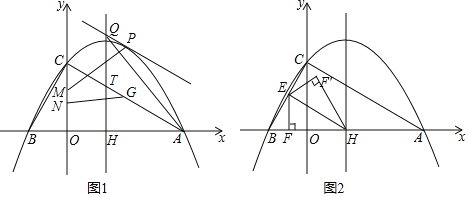
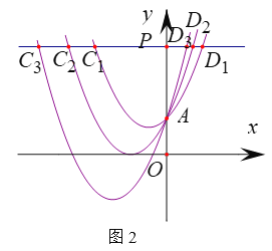
£®3£©ĶĪĶ„![]() ‘ŕ
‘ŕ![]() …Ō‘ň∂Į Ī£¨»ÁÕľ£®2£©ĻżĶ„
…Ō‘ň∂Į Ī£¨»ÁÕľ£®2£©ĻżĶ„![]() ◊ų
◊ų![]() £¨
£¨![]() ÷Š£¨īĻ◊„∑÷Īūő™
÷Š£¨īĻ◊„∑÷Īūő™![]() °Ę
°Ę![]() £¨…Ťĺō–ő
£¨…Ťĺō–ő![]() ”Ž
”Ž![]() ÷ōĶĢ≤Ņ∑÷√śĽżő™
÷ōĶĢ≤Ņ∑÷√śĽżő™![]() £¨«ů
£¨«ů![]() ”Ž
”Ž![]() ĶńļĮ żĻōŌĶ Ĺ£¨≤Ę«ů≥Ų
ĶńļĮ żĻōŌĶ Ĺ£¨≤Ę«ů≥Ų![]() Ķń◊Óīů÷Ķ£Ľ
Ķń◊Óīů÷Ķ£Ľ
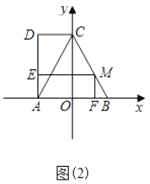
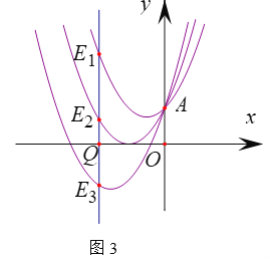
£®4£©»ÁÕľ£®3£©Ķ„![]() ‘ŕ£®1£©÷–ĶńŇ◊őÔŌŖ…Ō£¨
‘ŕ£®1£©÷–ĶńŇ◊őÔŌŖ…Ō£¨![]() «
«![]() —”≥§ŌŖ…ŌĶń“ĽĶ„£¨«“
—”≥§ŌŖ…ŌĶń“ĽĶ„£¨«“![]() °Ę
°Ę![]() ŃĹĶ„ĺý‘ŕĶ໿ŌůŌřńŕ£¨
ŃĹĶ„ĺý‘ŕĶ໿ŌůŌřńŕ£¨![]() °Ę
°Ę![]() «őĽ”ŕ÷ĪŌŖ
«őĽ”ŕ÷ĪŌŖ![]() Õ¨≤ŗĶń≤ĽÕ¨ŃĹĶ„£¨»ŰĶ„
Õ¨≤ŗĶń≤ĽÕ¨ŃĹĶ„£¨»ŰĶ„![]() ĶĹ
ĶĹ![]() ÷ŠĶńĺŗņŽő™
÷ŠĶńĺŗņŽő™![]() £¨
£¨![]() Ķń√śĽżő™
Ķń√śĽżő™![]() £¨«ůĶ„
£¨«ůĶ„![]() Ķń◊ÝĪÍ£ģ
Ķń◊ÝĪÍ£ģ
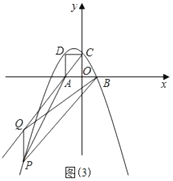
°ĺīūįł°Ņ£®1£©![]() £Ľ£®2£©Ķ„
£Ľ£®2£©Ķ„![]() ĽÚ
ĽÚ![]() £Ľ£®3£©
£Ľ£®3£©![]() £¨ĶĪ
£¨ĶĪ![]() Ī£¨
Ī£¨![]() ◊Óīů
◊Óīů![]() £Ľ£®4£©
£Ľ£®4£©![]()
°ĺĹ‚őŲ°Ņ
£®1£©”…÷ĪĹ«»żĹ«–őĶń–‘÷ Ņ…«ůĶ„C£¨Ķ„D◊ÝĪÍ£¨”…īż∂®ŌĶ ż∑®Ņ…«ůĹ‚őŲ Ĺ£Ľ
£®2£©”…»ęĶ»»żĹ«–őĶń–‘÷ Ņ…Ķ√DM=AM£¨PD=AP£¨Ņ…Ķ√Ķ„P‘ŕADĶńīĻ÷Ī∆Ĺ∑÷ŌŖ…Ō£¨Ņ…«ůĶ„PĶń◊›◊ÝĪÍ£¨īķ»ŽŅ…«ůĹ‚£Ľ
£®3£©”…Ő‚“‚Ņ…÷§°ųACB «Ķ»ĪŖ»żĹ«–ő£¨Ņ…Ķ√CM=2t-4£¨BF=![]() £®8-2t£©=4-t£¨MF=
£®8-2t£©=4-t£¨MF=![]() -
-![]() t£¨AF=t£¨ľīŅ…«ů÷ōĶĢ≤Ņ∑÷√śĽż£¨”…∂ĢīőļĮ żĶń–‘÷ Ņ…«ůĹ‚£Ľ
t£¨AF=t£¨ľīŅ…«ů÷ōĶĢ≤Ņ∑÷√śĽż£¨”…∂ĢīőļĮ żĶń–‘÷ Ņ…«ůĹ‚£Ľ
£®4£©Ō»«ů≥Ų÷ĪŌŖAC£¨BPĶńĹ‚őŲ Ĺ£¨ľīŅ…«ůĶ„P◊ÝĪÍ£ģ
Ĺ‚£ļ£®1£©°ŖňńĪŖ–ő![]() «ĺō–ő£¨
«ĺō–ő£¨
°ŗ![]() £¨
£¨![]() £¨«“
£¨«“![]() £¨
£¨![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗĶ„![]() £¨Ķ„
£¨Ķ„![]() £¨
£¨
…ŤŇ◊őÔŌŖĹ‚őŲ Ĺő™![]() £¨īķ
£¨īķ![]() £¨
£¨![]()
°ŗ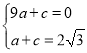 £¨
£¨
Ĺ‚Ķ√£ļ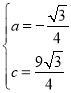 £¨
£¨
°ŗŇ◊őÔŌŖĹ‚őŲ Ĺő™![]() £Ľ
£Ľ
£®2£©°Ŗ![]() ő™
ő™![]() ÷–Ķ„£¨
÷–Ķ„£¨
°ŗ![]() £¨
£¨
°Ŗ°ųPAM°’°ųPDM£¨
°ŗ![]() £¨
£¨
°ŗĶ„![]() ‘ŕ
‘ŕ![]() ĶńīĻ÷Ī∆Ĺ∑÷ŌŖ…Ō£¨
ĶńīĻ÷Ī∆Ĺ∑÷ŌŖ…Ō£¨
°ŗĶ„![]() ◊›◊ÝĪÍő™
◊›◊ÝĪÍő™![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨![]() £¨
£¨
°ŗĶ„![]() ĽÚ
ĽÚ![]() £Ľ
£Ľ
£®3£©»ÁÕľ2£¨°Ŗ![]() £¨
£¨![]() £¨
£¨
°ŗ![]() £¨
£¨![]() £¨
£¨
°ŗ°ųACB «Ķ»ĪŖ»żĹ«–ő£¨
”…Ő‚“‚Ņ…Ķ√£ļ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £ģ
£ģ
°ŖňńĪŖ–ő![]() «ĺō–ő£¨
«ĺō–ő£¨
°ŗ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
°ŗ![]() £¨
£¨![]() £¨
£¨
°ŗ°ųCMH «Ķ»ĪŖ»żĹ«–ő£¨
°ŗ![]() £¨
£¨
°Ŗ![]() £¨
£¨
ĶĪ![]() Ī£¨
Ī£¨![]() ◊Óīů
◊Óīů![]() £Ľ
£Ľ
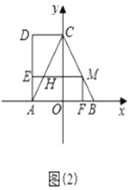
£®4£©°Ŗ![]() £¨”÷
£¨”÷![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
…Ť÷ĪŌŖ![]() Ĺ‚őŲ Ĺő™
Ĺ‚őŲ Ĺő™![]() £¨į—
£¨į—![]() £¨
£¨![]() īķ»Ž∆š÷–£¨
īķ»Ž∆š÷–£¨
Ķ√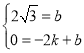 £¨
£¨
°ŗ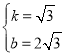 £¨
£¨
°ŗ÷ĪŌŖ![]() Ĺ‚őŲ Ĺő™£ļ
Ĺ‚őŲ Ĺő™£ļ![]() £¨
£¨
…Ť÷ĪŌŖ![]() ĶńĹ‚őŲ Ĺő™
ĶńĹ‚őŲ Ĺő™![]() £¨
£¨
į—![]() īķ»Ž∆š÷–£¨Ķ√
īķ»Ž∆š÷–£¨Ķ√![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ÷ĪŌŖ![]() Ĺ‚őŲ Ĺő™£ļ
Ĺ‚őŲ Ĺő™£ļ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £®…Š»•£©£¨
£®…Š»•£©£¨![]() £¨
£¨
°ŗ![]() £ģ
£ģ