题目内容
2.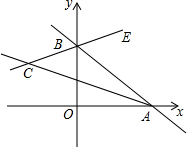 如图,在平面直角坐标系中,已知点A,点B分别是x,y轴的正半轴上的动点,BE是∠ABy的平分线.BE的反向处长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否会发生变化?如果变化,说明你的理由;如果不变,求出∠ACB的度数.
如图,在平面直角坐标系中,已知点A,点B分别是x,y轴的正半轴上的动点,BE是∠ABy的平分线.BE的反向处长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否会发生变化?如果变化,说明你的理由;如果不变,求出∠ACB的度数.
分析 根据三角形的外角的性质得到∠ABy-∠OAB=90°,∠ACB=∠ABE-∠CAB,根据角平分线的定义计算即可.
解答 解:∠ACB的大小不变,
∵∠ABy-∠OAB=90°,
∴$\frac{1}{2}$∠ABy-$\frac{1}{2}$∠OAB=45°,
∴∠ACB=∠ABE-∠CAB=$\frac{1}{2}$∠ABy-$\frac{1}{2}$∠OAB=45°.
答:∠ACB的度数是45°.
点评 本题考查的是三角形内角和定理、三角形的外角的性质和坐标与图形的关系,掌握三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.

练习册系列答案
相关题目
12. 若二次函数y=ax2+bx+a2-2(a,b为常数)的图象如图,则a的值为( )
若二次函数y=ax2+bx+a2-2(a,b为常数)的图象如图,则a的值为( )
 若二次函数y=ax2+bx+a2-2(a,b为常数)的图象如图,则a的值为( )
若二次函数y=ax2+bx+a2-2(a,b为常数)的图象如图,则a的值为( )| A. | 1 | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | -2 |
12.如果∠A是锐角,且sinA=cosA,那么∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.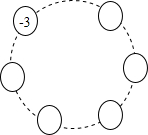 如图,请在小圆圈内填满数,使每个小圆圈里的数都是它两旁小圆圈里数的和,并求出所有小圆圈里数的和,如果把原来填的-3改成a,按上面的要求填满后,所有小圆圈里数的和又是多少?
如图,请在小圆圈内填满数,使每个小圆圈里的数都是它两旁小圆圈里数的和,并求出所有小圆圈里数的和,如果把原来填的-3改成a,按上面的要求填满后,所有小圆圈里数的和又是多少?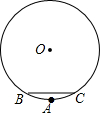 如图,某健身广场中心修建了一个圆形喷水池,数学活动小组为测量喷水池的半径,选取水池围栏上的A,B,C三根白玉石柱,量得AB=AC,BC长为14m,点A到BC的距离为1m,请你帮他们求出喷水池的半径.
如图,某健身广场中心修建了一个圆形喷水池,数学活动小组为测量喷水池的半径,选取水池围栏上的A,B,C三根白玉石柱,量得AB=AC,BC长为14m,点A到BC的距离为1m,请你帮他们求出喷水池的半径.