题目内容
已知方程3x2-5x+1=0的两根据分别为α,β,则3α2-6α-β+αβ= .
考点:根与系数的关系,一元二次方程的解
专题:
分析:先由方程3x2-5x+1=0的两根分别为α,β,根据一元二次方程的解的定义得出3α2-5α+1=0,即3α2=5α-1,根据根与系数的关系得出α+β=
,αβ=
,再将3α2-6α-β+αβ变形为-(α+β)+αβ-1,代入计算即可求解.
| 5 |
| 3 |
| 1 |
| 3 |
解答:解:∵方程3x2-5x+1=0的两根分别为α,β,
∴3α2-5α+1=0,α+β=
,αβ=
,
∴3α2=5α-1,
∴3α2-6α-β+αβ=5α-1-6α-β+αβ=-(α+β)+αβ-1=-
+
-1=-
.
故答案为-
.
∴3α2-5α+1=0,α+β=
| 5 |
| 3 |
| 1 |
| 3 |
∴3α2=5α-1,
∴3α2-6α-β+αβ=5α-1-6α-β+αβ=-(α+β)+αβ-1=-
| 5 |
| 3 |
| 1 |
| 3 |
| 7 |
| 3 |
故答案为-
| 7 |
| 3 |
点评:此题主要考查了一元二次方程的解的定义,根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
下列各组线段,能组成三角形的是( )
| A、2cm,3cm,5cm |
| B、5cm,6cm,10cm |
| C、1cm,1cm,3cm |
| D、3cm,4cm,8cm |
 如图,在⊙O的内接四边形ABCD中,DB=DC,∠DAE是四边形ABCD的一个外角.∠DAE与∠DAC相等吗?为什么?
如图,在⊙O的内接四边形ABCD中,DB=DC,∠DAE是四边形ABCD的一个外角.∠DAE与∠DAC相等吗?为什么? 如图,在△ABC中,AB=AC=10,BC=12,AH⊥BC于H,点P从点B出发沿射线BC以每秒3个单位长度的速度运动,点Q从点C出发沿CA边以每秒2个单位长度的速度向点A运动,DE保持垂直平分PQ,且交PQ于点D,交AH所在直线于点E.若P、Q两点同时出发,当点Q运动到点A时,P、Q两点停止运动,设运动时间为t秒(t>0).
如图,在△ABC中,AB=AC=10,BC=12,AH⊥BC于H,点P从点B出发沿射线BC以每秒3个单位长度的速度运动,点Q从点C出发沿CA边以每秒2个单位长度的速度向点A运动,DE保持垂直平分PQ,且交PQ于点D,交AH所在直线于点E.若P、Q两点同时出发,当点Q运动到点A时,P、Q两点停止运动,设运动时间为t秒(t>0).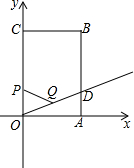 已知如图,矩形OABC在平面直角坐标系中,OA=
已知如图,矩形OABC在平面直角坐标系中,OA=