题目内容
16.若分式$\frac{x+1}{3x-2}$的值为正数,则x的取值范围是x>$\frac{2}{3}$或x<-1.分析 根据已知得出分式的分子与分母同号,进而得出不等式组求出答案.
解答 解:∵分式$\frac{x+1}{3x-2}$的值为正数,
∴$\left\{\begin{array}{l}{x+1>0}\\{3x-2>0}\end{array}\right.$或$\left\{\begin{array}{l}{x+1<0}\\{3x-2<0}\end{array}\right.$,
解得:x>$\frac{2}{3}$或x<-1.
故答案为:x>$\frac{2}{3}$或x<-1.
点评 此题主要考查了分式的值以及不等式组的解法,正确分类讨论得出是解题关键.

练习册系列答案
相关题目
7.判定两个等腰三角形全等的条件可以是( )
| A. | 有一腰和一角对应相等 | B. | 有两角一边对应相等 | ||
| C. | 有顶角和一个底角对应相等 | D. | 有两角对应相等 |
6.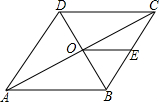 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为BC的中点,则下列等式中一定成立的是( )
如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为BC的中点,则下列等式中一定成立的是( )
 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为BC的中点,则下列等式中一定成立的是( )
如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为BC的中点,则下列等式中一定成立的是( )| A. | AB=BE | B. | AC=2AB | C. | AB=2OE | D. | AC=2OE |
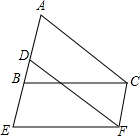 如图,将三角形ABC沿射线AB的方向平移2个单位到三角形DEF的位置,连接CF,点A,B,C的对应点分别是点D,E,F.
如图,将三角形ABC沿射线AB的方向平移2个单位到三角形DEF的位置,连接CF,点A,B,C的对应点分别是点D,E,F.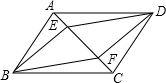 已知:如图,在四边形ABCD中,AB=CD,BC=AD,点E、F在AC上,且AF=CE.求证:四边形BEDF是平行四边形.
已知:如图,在四边形ABCD中,AB=CD,BC=AD,点E、F在AC上,且AF=CE.求证:四边形BEDF是平行四边形.