题目内容
14.对于一个腰长为5、底边长为6的等腰三角形,请建立适当的直角坐标系,并在图中标出各个顶点的坐标.分析 以AB所在的直线为x轴,以AB边上的高所在的直线为y轴,建立平面直角坐标系,则BO=AO,再根据勾股定理求出CO的长度,点A、B、C的坐标即可写出.
解答  解:如图,以AB所在的直线为x轴,以AB边上的高所在的直线为y轴,建立平面直角坐标系,
解:如图,以AB所在的直线为x轴,以AB边上的高所在的直线为y轴,建立平面直角坐标系,
等腰三角形ABC的腰长为5,底长为6,
∴AO=BO=3,
∴点A、B的坐标分别为A(-3,0),B(3,0),
∵CO=$\sqrt{A{C}^{2}-A{O}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴点C的坐标为(0,4).
点评 本题主要考查等腰三角形的性质和勾股定理的运用,建立适当的平面直角坐标系是解题的关键.

练习册系列答案
相关题目
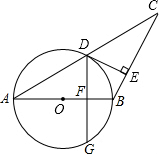 如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,求证:DE是⊙O的切线.
如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,求证:DE是⊙O的切线.