题目内容
2.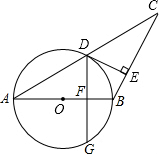 如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,求证:DE是⊙O的切线.
如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,求证:DE是⊙O的切线.
分析 连接DO,首先证明DO∥BC,根据平行线的性质可得∠DEC=∠ODE=90°,从而可得结论.
解答  证明:连接DO,
证明:连接DO,
∵AB=BC,
∴∠CAB=∠C,
∵AO=DO,
∴∠CAB=∠ADO,
∴∠C=∠ADO,
∴DO∥BC,
∴∠DEC=∠ODE,
∵DE⊥BC,
∴∠DEC=90°,
∴∠ODE=90°,
∴DO⊥DE,
∴DE是⊙O的切线.
点评 此题主要考查了切线的判定,关键是掌握经过半径的外端且垂直于这条半径的直线是圆的切线.

练习册系列答案
相关题目
12.下列代数式:是单项式为( )
| A. | $\frac{b}{a}$ | B. | $\frac{x-y}{5}$ | C. | 2π | D. | x+1 |
13.下列结论正确的是( )
| A. | 0是正数也是有理数 | |
| B. | 两数之积为正,这两数同为正 | |
| C. | 几个数相乘,积的符号由负因数的个数决定 | |
| D. | 互为相反数的两个数的绝对值相等 |
11.一次函数y=2x+3的图象过A(-1,y1),B(3,y2)两点,则y1与y2的大小关系为( )
| A. | y1>y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1≤y2 |
 如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米,求CE的长3厘米.
如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米,求CE的长3厘米.