题目内容
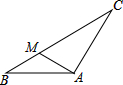 如图,在△ABC中,AB=AC,∠BAC=120°,点M在边BC上,AM=BM.求证:CM=2BM.
如图,在△ABC中,AB=AC,∠BAC=120°,点M在边BC上,AM=BM.求证:CM=2BM.考点:含30度角的直角三角形,等腰三角形的判定与性质
专题:证明题
分析:根据等腰三角形性质和三角形内角和定理求出∠B=∠C=30°,求出∠MAB=30°,求出∠MAC度数,推出CM=2AM,即可得出答案.
解答:证明:∵在△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AM=BM,
∴∠MAB=∠B=30°,
∴∠MAC=120°-30°=90°,
∵∠C=30°,
∴CM=2AM=2BM.
∴∠B=∠C=30°,
∵AM=BM,
∴∠MAB=∠B=30°,
∴∠MAC=120°-30°=90°,
∵∠C=30°,
∴CM=2AM=2BM.
点评:本题考查了等腰三角形性质,三角形的内角和定理,含30度角的直角三角形的性质的应用,能求出∠C=30°和∠MAC=90°是解此题的关键.

练习册系列答案
相关题目
 如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A、美 | B、丽 | C、泸 | D、州 |
 如图,化简|a+b|-|a|+|b|=
如图,化简|a+b|-|a|+|b|= 已知:如图,抛物线y=ax2+bx+c经过A(1,0),B(5,0),C(0,5)三点.
已知:如图,抛物线y=ax2+bx+c经过A(1,0),B(5,0),C(0,5)三点.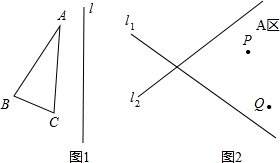 (1)画出图1中△ABC关于直线L的对称图形△A′B′C′.
(1)画出图1中△ABC关于直线L的对称图形△A′B′C′.