题目内容
两个正多边形的边数之比为1:2,内角和之比为3:8,求这两个多边形的边数、内角和.
考点:多边形内角与外角
专题:
分析:根据多边形的内角和公式则有两多边形的内角和分别为180(n-2)°和180(2n-2)°,进而利用内角和之比为3:8,求出即可.
解答:解:设这两个正多边形的边数分别为n和2n条,
根据多边形的内角和公式则有两多边形的内角和分别为180(n-2)°和180(2n-2)°,
由于两内角和度数之比为3:8,
因此
=
,
解得:n=5,
则180(n-2)=540°,180(2n-2)=1440°,
所以这两多边形的内角和分别为540°和1440°.
根据多边形的内角和公式则有两多边形的内角和分别为180(n-2)°和180(2n-2)°,
由于两内角和度数之比为3:8,
因此
| 180(n-2) |
| 3 |
| 180(2n-2) |
| 8 |
解得:n=5,
则180(n-2)=540°,180(2n-2)=1440°,
所以这两多边形的内角和分别为540°和1440°.
点评:此题主要考查了多边形内角与外角,根据已知得出
=
,求出多边形边数是解题关键.
| 180(n-2) |
| 3 |
| 180(2n-2) |
| 8 |

练习册系列答案
相关题目
若3(x+1)2-48=0,则x的值等于( )
| A、±4 | B、3或-5 |
| C、-3或5 | D、3或5 |
符号“f”表示一种运算,它对一些数的运算结果如下:
(1)f(1)=0,f(2)=1,f(3)=2,f(4)=3,…
(2)f(
)=2,f(
)=3,f(
)=4,f(
)=5,…
利用以上规律计算f(
)-f(2015)结果是( )
(1)f(1)=0,f(2)=1,f(3)=2,f(4)=3,…
(2)f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
利用以上规律计算f(
| 1 |
| 2014 |
| A、-1 | B、0 | C、1 | D、不能确定 |
由二次函数y=2x2-12x+20,可知正确的是( )
| A、其图象的开口向下 |
| B、其图象的对称轴为直线x=-3 |
| C、其最小值为2 |
| D、当x≤3时,y随x的增大而增大 |
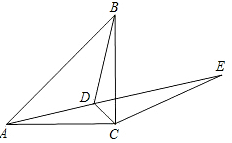 如图,在△ABC中,∠ACB=90°,AC=BC,点D为△ABC内一点,∠CAD=∠CBD=15°,点E为AD延长线上的一点,且CE=AC.
如图,在△ABC中,∠ACB=90°,AC=BC,点D为△ABC内一点,∠CAD=∠CBD=15°,点E为AD延长线上的一点,且CE=AC. 如图,△ABC和△ECD均为等边三角形,B、C、D三点在一直线上,AD、BE相交于点F,DF=3,AF=4,则线段FE的长为
如图,△ABC和△ECD均为等边三角形,B、C、D三点在一直线上,AD、BE相交于点F,DF=3,AF=4,则线段FE的长为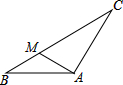 如图,在△ABC中,AB=AC,∠BAC=120°,点M在边BC上,AM=BM.求证:CM=2BM.
如图,在△ABC中,AB=AC,∠BAC=120°,点M在边BC上,AM=BM.求证:CM=2BM.