题目内容
9.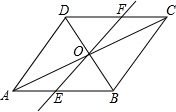 如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的动直线交AB于E,交CD于F.求证:OE=OF.
如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的动直线交AB于E,交CD于F.求证:OE=OF.
分析 由平行四边形的对边平行且相等,得到DC与AB平行,利用两直线平行内错角相等得到两对角相等,再由对角线互相平分得到OD=OB,利用AAS得到三角形DOF与三角形BOE全等,利用全等三角形对应边相等即可得证.
解答 证明:∵平行四边形ABCD,
∴OD=OB,DC∥AB,
∴∠FDO=∠EBO,∠DFO=∠OEB,
在△DOF和△BOE中,
$\left\{\begin{array}{l}{∠DFO=∠EBO}\\{∠DFO=∠BEO}\\{OD=OB}\end{array}\right.$,
∴△DOF≌△BOE(AAS),
∴OE=OF.
点评 此题考查了平行四边形的性质,全等三角形的判定与性质,熟练掌握平行四边形的性质是解本题的关键.

练习册系列答案
相关题目
14.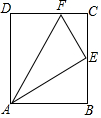 折叠矩形ABCD,使点D落在BC的边上点E处,并使折痕经过点A交CD于点F,若点E恰好为BC的中点,则CE:CF等于( )
折叠矩形ABCD,使点D落在BC的边上点E处,并使折痕经过点A交CD于点F,若点E恰好为BC的中点,则CE:CF等于( )
 折叠矩形ABCD,使点D落在BC的边上点E处,并使折痕经过点A交CD于点F,若点E恰好为BC的中点,则CE:CF等于( )
折叠矩形ABCD,使点D落在BC的边上点E处,并使折痕经过点A交CD于点F,若点E恰好为BC的中点,则CE:CF等于( )| A. | $\sqrt{3}$:1 | B. | 5:2 | C. | $\sqrt{2}$:1 | D. | 2:1 |
1.下列方程中,是二元一次方程的是( )
| A. | xy-2x=1 | B. | 3x+1=y | C. | y=9 | D. | 6x+y2=7 |

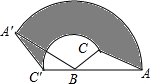 如图,在△ABC中,AB=6cm,BC=3cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的点C处,那么AC边扫过的图形(图中阴影部分)的面积是$\frac{45}{4}$πcm2.
如图,在△ABC中,AB=6cm,BC=3cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的点C处,那么AC边扫过的图形(图中阴影部分)的面积是$\frac{45}{4}$πcm2.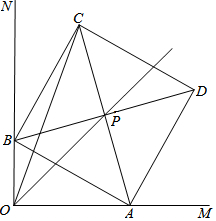 已知∠MON=90°,线段AB长为6cm,AB两端分别在OM、ON上滑动,以AB为边作正方形ABCD,对角线AC、BD相交于点P,连结OC.
已知∠MON=90°,线段AB长为6cm,AB两端分别在OM、ON上滑动,以AB为边作正方形ABCD,对角线AC、BD相交于点P,连结OC.