题目内容
已知关于x的一元二次方程mx2﹣(m+2)x+2=0.
(1)证明:不论m为何值时,方程总有实数根;
(2)m为何整数时,方程有两个不相等的正整数根.
(1)证明见解析;(2)m=1. 【解析】试题分析:(1)求出方程根的判别式,利用配方法进行变形,根据平方的非负性证明即可; (2)利用一元二次方程求根公式求出方程的两个根,根据题意求出m的值. (1)证明:△=(m+2)2﹣8m =m2﹣4m+4 =(m﹣2)2, ∵不论m为何值时,(m﹣2)2≥0, ∴△≥0, ∴方程总有实数根; (2)【...
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


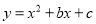 的图象经过点
的图象经过点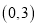 ,
, 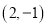 .
.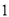 )求
)求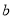 ,
, 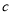 的值.
的值.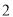 )求该二次函数图象的对称轴及与
)求该二次函数图象的对称轴及与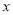 轴交点坐标.
轴交点坐标.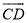 上的一个动点,连接AP,则AP长的最小值是 .
上的一个动点,连接AP,则AP长的最小值是 .
 B.
B. 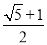 C.
C. 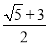 D.
D. 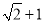
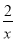 ﹣1=0 B. 5x2﹣6y﹣3=0 C. ax2﹣x+2=0 D. 3x2﹣2x﹣1=0
﹣1=0 B. 5x2﹣6y﹣3=0 C. ax2﹣x+2=0 D. 3x2﹣2x﹣1=0 的解集表示在数轴上,正确的是( )
的解集表示在数轴上,正确的是( )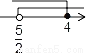 B.
B. 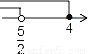 C.
C. 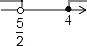 D.
D. 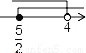
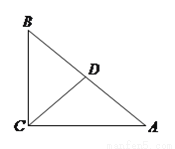
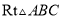 中,
中, 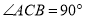 ,点
,点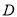 在
在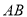 上,
上, 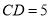 ,
, 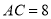 ,
, 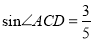 ,则
,则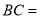 __________.
__________.
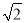 x+m=0有两个不相等的实数根.
x+m=0有两个不相等的实数根.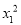 +
+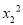 -
-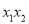 的值.
的值.