题目内容
19．
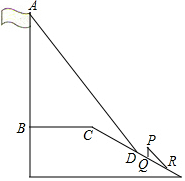某中学广场上的旗杆AB，在某一时刻它的影子一部分落在平台上，另一部分落在斜坡上，测得落在平台上的影长BC为3米，落在斜坡上的影长CD为2米，AB⊥BC，同一时刻，光线与水平面的夹角为60°，1米的竖立标杆PQ在斜坡上的影长QR为2米，求旗杆的高度（若结果中有根号，请保留根号）
分析 直接利用已知得出对应边的比值相等，进而求出CM的长，再求出AN的长进而得出答案．
解答 
解：如图作CM∥AB交AD于M，MN⊥AB于N．
由题意得：$\frac{CM}{CD}$=$\frac{PQ}{QR}$，
得 CM=1，
在Rt△AMN中，
∵∠ANM=90°，MN=BC=3，∠AMN=60°，
∴AN=3$\sqrt{3}$，
∵MN∥BC，AB∥CM，
∴四边形MNBC是平行四边形，
∴BN=CM=1，
∴AB=AN+BN=（1+3$\sqrt{3}$）米．
点评 此题主要考查了解直角三角形的应用，正确得出BN的长是解题关键．
练习册系列答案
相关题目
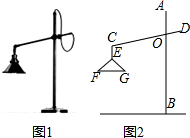如图1所示的是一种置于桌面上的简易台灯，将其结构简化成图2，灯杆AB与CD交于点O（点O固定），灯罩连杆CE始终保持与AB平行，灯罩下方FG处于水平位置，测得OC=20cm，∠COB=70°，∠F=40°，EF=EG，点G到OB的距离为14cm．
如图，已知△ABC中，AB=AC，把△ABC绕A点沿顺时针方向旋转得到△ADE，连接BD，CE交于点F．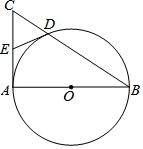
如图，在Rt△ABC中，∠CAB=90°，以AB为直径的⊙O交BC于点D，点E是AC的中点，连接DE．