题目内容
6.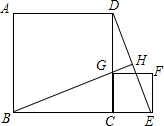 如图,正方形ABCD的边长为1,G为CD边上一动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.
如图,正方形ABCD的边长为1,G为CD边上一动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.求证:①△BCG≌△DCE;②BH⊥DE.
分析 (1)根据正方形的边的性质和直角可通过SAS判定△BCG≌△DCE,
(2)利用全等的性质得到∠BHD=90°即BH⊥DE.
解答 证明:(1)在正方形ABCD中,∠BCG=90°,BC=CD
在正方形GCEF中,∠DCE=90°,CG=CE
在△BCG和△DCE中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCG=∠DCE}\\{CG=CE}\end{array}\right.$,
∴△BCG≌△DCE(SAS)
(2)∵△BCG≌△DCE,
∴∠1=∠2,
∵∠2+∠DEC=90°
∴∠1+∠DEC=90°
∴∠BHD=90°
∴BH⊥DE;
点评 此题主要考查正方形的性质,全等三角形的判定等知识,解题的关键是正确寻找全等三角形,学会利用“8字型”证明直角.属于中考常考题型.

练习册系列答案
相关题目
16.已知a-b=5,ab=-2,则代数式a2+b2-1的值是( )
| A. | 16 | B. | 18 | C. | 20 | D. | 28 |
14.下列各题中正确的是( )
| A. | 由7x=4x-3移项得7x-4x=3 | |
| B. | 由$\frac{2x-1}{3}$=1+$\frac{x-3}{2}$去分母得2(2x-1)=1+3(x-3) | |
| C. | 由2(2x-1)-3(x-3)=1去括号得4x-2-3x-9=1 | |
| D. | 由2(x+1)=x+7 移项、合并同类项得 x=5 |
11.有理数-32,(-3)2,|-33|按从小到大的顺序排列是( )
| A. | |-33|<-32<(-3)2 | B. | |-33|<(-3)2<-32 | C. | -32<|-33|<(-3)2 | D. | -32<(-3)2<|-33| |
18.使二次根式$\sqrt{x-2}$有意义的x的取值范围是( )
| A. | x>0 | B. | x>2 | C. | x≥2 | D. | x≠2 |
15.计算2a2b-3a2b的正确结果是( )
| A. | ab2 | B. | -ab2 | C. | a2b | D. | -a2b |
16.在墙壁上用两个钉子就能固定一根横放的木条,这样做根据的道理是( )
| A. | 两点确定一条直线 | B. | 两点确定一条线段 | ||
| C. | 两点之间,直线最短 | D. | 两点之间,线段最短 |
 二次函数y=ax2+bx+c(a≠0)的图象的一部分,则一元二次方程的两根分别为x1=-1,x2=3.
二次函数y=ax2+bx+c(a≠0)的图象的一部分,则一元二次方程的两根分别为x1=-1,x2=3.