二次函数y=ax2+bx+c的图象的一部分.则一元二次方程的两根分别为x1=-1.x2=3．题目和参考答案——青夏教育精英家教网—

题目内容

1．

二次函数y=ax²+bx+c（a≠0）的图象的一部分，则一元二次方程的两根分别为x₁=-1，x₂=3．

分析一元二次方程ax²+bx+c=0的解就是二次函数y=ax²+bx+c（a，b，c是常数，a≠0）与x轴的交点横坐标．

解答解：∵抛物线对称轴为x=1，与X轴的一个交点为（-1，0），
∴另一个交点为（3，0），
∴ax²+bx+c=0的解为：x₁=-1，x₂=3，
故答案为：x₁=-1，x₂=3．

点评此题主要考查了抛物线与x轴的交点，关键是掌握求二次函数y=ax²+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y=0，即ax²+bx+c=0，解关于x的一元二次方程即可求得交点横坐标．

练习册系列答案

相关题目

11．已知关于x的方程x²+2x=m有两个相等的实数根，则m的值是（　　）

12．求下列各式的值．
（1）$\sqrt{{{（-4）}^2}}$-$\root{{{\;}^3}}{-8}$+$\sqrt{1\frac{9}{16}}$；
（2）（-3）²-$\sqrt{{{10}^{-2}}}$+$\root{{{\;}^3}}{27}$．

9．已知关于x，y的二元一次方程组$\left\{\begin{array}{l}{ax-y+b=0}\\{y=kx}\end{array}\right.$（a，b，k均为常数，且a≠0，k≠0）的解为$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$，则直线y=ax+b和直线y=kx的交点坐标为（-4，-2）．

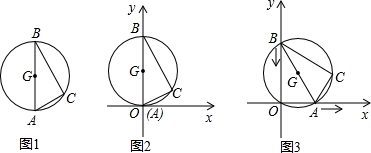
16．图1是用钢丝制作的一个几何探究工具，其中△ABC内接于⊙G，AB是⊙G的直径，AB=6，AC=2．现将制作的几何探究工具放在平面直角坐标系中（如图2），然后点A在射线OX上由点O开始向右滑动，点B在射线OY上也随之向点O滑动（如图3），当点B滑动至与点O重合时运动结束．在整个运动过程中，点C运动的路程是（　　）

6．

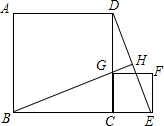如图，正方形ABCD的边长为1，G为CD边上一动点（点G与C、D不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE交BG的延长线于点H．
求证：①△BCG≌△DCE；②BH⊥DE．

13．已知m是系数，关于x、y的两个多项式mx²-2x+y与-3x²+2x+3y的差中不含二次项，则代数式m²+3m-1的值为-1．

10．某地下车库出口处安装了“两段式栏杆”，如图1所示，点A是栏杆转动的支点，点E是栏杆两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计），其中AB⊥BC，EF∥BC，∠AEF=143°，AB=AE=1.2米，那么适合该地下车库的车辆限高标志牌为多少米？（结果精确到0.1．参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75）

11．若a＜0，则下列结论不正确的是（　　）

a²=|a|²

试题分类