题目内容
已知函数y=(m2+2m)xm2+m-1-2是一次函数,它的图象与反比例函数y=
的图象交于一点,交点的横坐标是
,求反比例函数的解析式.
| k |
| x |
| 1 |
| 3 |
考点:反比例函数与一次函数的交点问题
专题:
分析:根据一次函数的定义可得
,由此求出m的值,得到一次函数的解析式,再求出交点的纵坐标,然后把交点的坐标代入反比例函数的解析式,即可求出k的值.
|
解答:解:∵函数y=(m2+2m)xm2+m-1-2是一次函数,
∴
,
∴
,
∴m=1,
∴一次函数是y=3x-2.
当x=
时,则y=-1.
即交点坐标是(
,-1).
把它代入反比例函数解析式,得
k=
×(-1)=-
,
∴反比例函数的解析式为y=-
.
∴
|
∴
|
∴m=1,
∴一次函数是y=3x-2.
当x=
| 1 |
| 3 |
即交点坐标是(
| 1 |
| 3 |
把它代入反比例函数解析式,得
k=
| 1 |
| 3 |
| 1 |
| 3 |
∴反比例函数的解析式为y=-
| 1 |
| 3x |
点评:本题考查的是一次函数的定义及用待定系数法求反比例函数的解析式,是中学阶段的重点.

练习册系列答案
相关题目
 如图,点D是线段AB的中点,点C是线段AD的中点,若CD=1cm,则线段AB=( )cm.
如图,点D是线段AB的中点,点C是线段AD的中点,若CD=1cm,则线段AB=( )cm.| A、1 | B、2 | C、4 | D、8 |
如果(an•bm•b)3=a9b15,那么m,n的值等于( )
| A、m=9,n=-4 |
| B、m=3,n=4 |
| C、m=4,n=3 |
| D、m=9,n=6 |
 如图,△ABC绕点B顺时针旋转到△EBD位置,若∠A=30°,∠D=15°,A、B、D在同一直线上,则旋转的角度是( )
如图,△ABC绕点B顺时针旋转到△EBD位置,若∠A=30°,∠D=15°,A、B、D在同一直线上,则旋转的角度是( )| A、50° | B、45° |
| C、40° | D、30° |
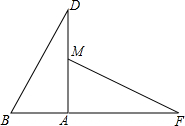 有两块相同的直角三角板如图1般放置,其中∠B=60°,∠F=30°,将△ABD绕直角顶点A顺时针旋转得到△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK的等腰三角形时,旋转角β的度数为
有两块相同的直角三角板如图1般放置,其中∠B=60°,∠F=30°,将△ABD绕直角顶点A顺时针旋转得到△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK的等腰三角形时,旋转角β的度数为