题目内容
18.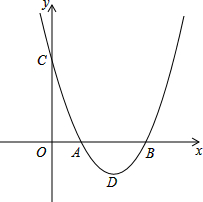 已知:抛物线y=x2+bx+c与x轴的两个交点分别为A(1,0)和B(3,0),与y轴交于点C.
已知:抛物线y=x2+bx+c与x轴的两个交点分别为A(1,0)和B(3,0),与y轴交于点C.(1)求此二次函数的解析式;
(2)写出点C的坐标(0,3),顶点D的座标为(2,-1);
(3)将直线CD沿y轴向下平移3个单位长度,求平移后直线m的解析式;
(4)在直线m上是否存在一点E,使得以点E、A、B、C为顶点的四边形是梯形?如果存在,请直接写出所有满足条件的E点的坐标(-1,2)或(-1.5,3)(不必写出过程)
分析 (1)把A与B坐标代入抛物线解析式求出b与c的值,即可确定出二次函数解析式;
(2)对于二次函数解析式,令x=0求出y的值,即可确定出C的坐标,由解析式确定出顶点坐标即可;
(3)利用待定系数法确定出直线CD解析式,利用平移规律确定出直线m的解析式即可;
(4)存在,利用梯形的性质及坐标与图形性质确定出E坐标即可.
解答 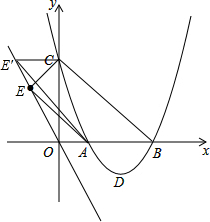 解:(1)∵抛物线y=x2+bx+c与x轴的两个交点分别为A(1,0)和B(3,0),
解:(1)∵抛物线y=x2+bx+c与x轴的两个交点分别为A(1,0)和B(3,0),
∴把A与B坐标代入得:$\left\{\begin{array}{l}{b+c+1=0}\\{3b+c+9=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-4}\\{c=3}\end{array}\right.$,
则二次函数解析式为y=x2-4x+3;
(2)对于y=x2-4x+3=(x-2)2-1,
令x=0,得到y=3,即C(0,3),顶点D(2,-1);
(3)设直线CD解析式为y=kx+b,
把C与D坐标代入得:$\left\{\begin{array}{l}{b=3}\\{2k+b=-1}\end{array}\right.$,
解得:k=-2,b=3,即直线CD解析式为y=-2x+3,
由平移规律得:平移后直线m的解析式为y=-2x;
(4)在直线m上存在一点E,使得以点E、A、B、C为顶点的四边形是梯形,
分两种情况考虑:若AE∥BC,可得直线BC与直线AE斜率相等,
设直线BC解析式为y=ax+b,
把B(3,0),C(0,3)代入得:$\left\{\begin{array}{l}{3a+b=0}\\{b=3}\end{array}\right.$,
解得:a=-1,b=3,
∴直线BC解析式为y=-x+3;
∴直线AE解析式为y=-(x-1)=-x+1,
联立得:$\left\{\begin{array}{l}{y=-x+1}\\{y=-2x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$,
此时E坐标为(-1,2);
若CE′∥AB,此时E′的纵坐标为3,即E′(-1.5,3),
综上,E的坐标为(-1,2)或(-1.5,3).
故答案为:(2)(0,3);(2,-1);(4)(-1,2)或(-1.5,3)
点评 此题属于二次函数综合题,涉及的知识有:待定系数法确定一次函数解析式,二次函数解析式,抛物线的顶点坐标,平移的性质,以及梯形的性质,熟练掌握待定系数法是解本题的关键.

 计算高手系列答案
计算高手系列答案(1)求a,b的值;
(2)一条开口向下,顶点为原点,且对称轴为y轴的抛物线恰好经过点M(2a,2a-b),求这条抛物线对应的函数表达式.
| A. | 2.18×109元 | B. | 21.8×108元 | C. | 2.176×109元 | D. | 21.76×108元 |
| A. | 两条对角线相等 | B. | 两条对角线相互垂直 | ||
| C. | 两条对角线相互垂直平分 | D. | 两条对角线相等且垂直 |
| A. | x<$\frac{2}{3}$ | B. | x≤$\frac{2}{3}$ | C. | x>$\frac{2}{3}$ | D. | x≥$\frac{2}{3}$ |

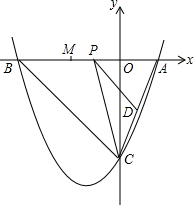 已知:如图,抛物线y=a(x+1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(2,0).
已知:如图,抛物线y=a(x+1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(2,0). 如图,矩形OABC,OA=9,AB=15,点E是BC上一点,沿AE折叠,使点B恰好落在x轴的点D处.
如图,矩形OABC,OA=9,AB=15,点E是BC上一点,沿AE折叠,使点B恰好落在x轴的点D处.