题目内容
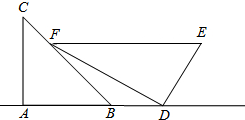 小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=4.
小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=4.(1)试求两平行线EF与AD之间的距离;
(2)试求BD的长.
考点:平行线之间的距离,等腰直角三角形
专题:
分析:(1)根据平行线的性质,可得∠F的度数,根据余弦函数,可得答案;
(2)根据平行线间的据相等,可得FH的长,根据等腰直角三角形的性质,可得BH的长,根据角的和差,可得∠FDH的长,根据余弦函数,可得DH的长,根据线段的和差,可得答案.
(2)根据平行线间的据相等,可得FH的长,根据等腰直角三角形的性质,可得BH的长,根据角的和差,可得∠FDH的长,根据余弦函数,可得DH的长,根据线段的和差,可得答案.
解答: 解:(1)过E作EG⊥AB于G,作FH⊥AB于H,
解:(1)过E作EG⊥AB于G,作FH⊥AB于H,
∵EF∥AD,∠E=60°,
∴∠EDG=60°,
∵DE=4,
∴EG=DEcos∠EDG=4×
=2
,
即两平行线EF与AD之间的距离为2
;
(2)∵EF∥AD,
∴FH=2
.
∵∠FNH=45°,∠FHB=90°,
∴HB=FH=2
.
∵∠EDF=90°,∠EDG=60°,
∴∠FDH=180°-∠EDF-∠FDG=180°-90°-60°=30°,
FD=2FH=4
,
DH=FD•cos∠FDH=4
×
=6,
BD=DH-BH=6-2
.
 解:(1)过E作EG⊥AB于G,作FH⊥AB于H,
解:(1)过E作EG⊥AB于G,作FH⊥AB于H,∵EF∥AD,∠E=60°,
∴∠EDG=60°,
∵DE=4,
∴EG=DEcos∠EDG=4×
| ||
| 2 |
| 3 |
即两平行线EF与AD之间的距离为2
| 3 |
(2)∵EF∥AD,
∴FH=2
| 3 |
∵∠FNH=45°,∠FHB=90°,
∴HB=FH=2
| 3 |
∵∠EDF=90°,∠EDG=60°,
∴∠FDH=180°-∠EDF-∠FDG=180°-90°-60°=30°,
FD=2FH=4
| 3 |
DH=FD•cos∠FDH=4
| 3 |
| ||
| 2 |
BD=DH-BH=6-2
| 3 |
点评:本题考查了平行线间的距离,(1)利用了平行线的性质,锐角三角函数;(2)利用了平行线间的距离相等,锐角三角函数,线段的和差.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若关于x的一元二次方程(k-1)x2-3
x=0有实数根,则k的取值范围是( )
| k |
A、k≥-
| ||
B、k>-
| ||
C、k≥-
| ||
| D、k≥O且k≠1 |
将方程
-
=2进行变形,结果正确的是( )
| x+4 |
| 0.2 |
| x-3 |
| 0.5 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、5(x+4)-2(x-3)=2 |
地球七大洲的总面积约是149 480 000km2,对这一数据精确到10000000可表示为( )
| A、149km2 |
| B、1.5×108km2 |
| C、1.49×108km2 |
| D、1.50×108km2 |
下列物体的运动不是旋转的是( )
| A、坐在摩天轮里的小朋友 |
| B、正在走动的时针 |
| C、骑自行车的人 |
| D、正在转动的风车叶片 |
 一条排水管的截面如图所示,已知该排水管的半径OA=10,水面宽AB=16,则排水管内水的最大深度CD的长为( )
一条排水管的截面如图所示,已知该排水管的半径OA=10,水面宽AB=16,则排水管内水的最大深度CD的长为( )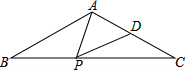 如图,已知△ABC中,AB=AC=2,∠B=30°,D为AC的中点,P是BC上的一动点,求PA+PD的最小值为( )
如图,已知△ABC中,AB=AC=2,∠B=30°,D为AC的中点,P是BC上的一动点,求PA+PD的最小值为( )
 如图,已知AD∥BC,∠1=∠2,说明∠3与∠4有什么关系,并说明理由.
如图,已知AD∥BC,∠1=∠2,说明∠3与∠4有什么关系,并说明理由.