题目内容
如图所示,已知: ,则
,则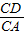 = ,
= , = ;若AD=2cm,则CD= cm;若BE=10cm,则AB= cm;若△ABC的周长是15cm,则△ADE的周长= cm.
= ;若AD=2cm,则CD= cm;若BE=10cm,则AB= cm;若△ABC的周长是15cm,则△ADE的周长= cm.
【答案】分析:由已知条件求得CD=AD+AC= AC,所以易求
AC,所以易求 =
= ;根据相似三角形的判定定理(对应边成比例,两个三角形相似)可知,
;根据相似三角形的判定定理(对应边成比例,两个三角形相似)可知,
△ADE∽△ACB,然后由相似三角形的周长比等于相似比可求得 ,从而知△ADE的周长.
,从而知△ADE的周长.
解答:解:∵ =
= =
= =
= ,
,
∴AD= AC,
AC,
∴CD=AD+AC= AC,
AC,
∴ =
= ;
;
当AD=2cm时,
CD=5cm;
当BE=10cm时,
AB=6cm;
∵ ,
,
∴△ADE∽△ACB(对应边成比例,两个三角形相似),
∴ =
= (相似三角形的周长的比等于相似比);
(相似三角形的周长的比等于相似比);
当△ABC的周长是15cm时,
△ADE的周长= ×15=10(cm).
×15=10(cm).
故答案为: ;
; ;5;6;10.
;5;6;10.
点评:本题主要考查了相似三角形的判定与性质.解答此题的关键是利用相似三角形的判定定理:对应边成比例,两个三角形相似,证明△ADE∽△ACB,然后根据相似三角形的性质解答后面的问题.
 AC,所以易求
AC,所以易求 =
= ;根据相似三角形的判定定理(对应边成比例,两个三角形相似)可知,
;根据相似三角形的判定定理(对应边成比例,两个三角形相似)可知,△ADE∽△ACB,然后由相似三角形的周长比等于相似比可求得
 ,从而知△ADE的周长.
,从而知△ADE的周长.解答:解:∵
 =
= =
= =
= ,
,∴AD=
 AC,
AC,∴CD=AD+AC=
 AC,
AC,∴
 =
= ;
;当AD=2cm时,
CD=5cm;
当BE=10cm时,
AB=6cm;
∵
 ,
,∴△ADE∽△ACB(对应边成比例,两个三角形相似),
∴
 =
= (相似三角形的周长的比等于相似比);
(相似三角形的周长的比等于相似比);当△ABC的周长是15cm时,
△ADE的周长=
 ×15=10(cm).
×15=10(cm).故答案为:
 ;
; ;5;6;10.
;5;6;10.点评:本题主要考查了相似三角形的判定与性质.解答此题的关键是利用相似三角形的判定定理:对应边成比例,两个三角形相似,证明△ADE∽△ACB,然后根据相似三角形的性质解答后面的问题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目


 如图所示,已知反比例函数y=
如图所示,已知反比例函数y=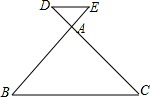 如图所示,已知:
如图所示,已知: ,则
,则 =________,
=________,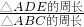 =________;若AD=2cm,则CD=________cm;若BE=10cm,则AB=________cm;若△ABC的周长是15cm,则△ADE的周长=________cm.
=________;若AD=2cm,则CD=________cm;若BE=10cm,则AB=________cm;若△ABC的周长是15cm,则△ADE的周长=________cm.