题目内容
1.观察下面的算式,1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;1+3+5+7+9=25=52…则1+3+5+7+9+…+13=49; 1+3+5+7+9+…+(2n-1)+(2n+1)=(n+1)2;41+43+45+…+77+79=1200.分析 观察题中已知:是从1开始的奇数求和,结果为自然数的平方,若算式的最后一个为2n+1,结果恰是(n+1)2,由此可以求解.
解答 解:已知是从1开始的奇数求和,结果为自然数的平方,若算式的最后一个为2n+1,结果恰是(n+1)2;
1+3+5+7+9+…+13=72=49;
1+3+5+7+9+…+(2n-1)+(2n+1)=(n+1)2;
41+43+45+…+77+79=1+3+5+7+9+…+77+79-(1+3+5+7+9+…+39)=402-202=1200.
故答案为:49,(n+1)2,1200.
点评 此题主要考查数列的规律探索与运用,观察已知找到存在的规律,并准确应用是解题的关键.

练习册系列答案
相关题目
12.下列交通标志中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.若关于x的分式方程$\frac{x}{x-5}$=3+$\frac{a}{5-x}$无解,则a的值为( )
| A. | a=5 | B. | a=-5 | C. | a=$\frac{1}{5}$ | D. | a=-$\frac{1}{5}$ |
6.下列等式中,不是整式的是( )
| A. | $x-\frac{1}{2}y$ | B. | $\frac{3}{7}x$ | C. | $\frac{1}{x-1}$ | D. | 0 |
 如图,AB是⊙O的直径,D是⊙O上一点,过点D作⊙O的切线交AB的延长线于点C,若∠C=20°,求∠A的度数.
如图,AB是⊙O的直径,D是⊙O上一点,过点D作⊙O的切线交AB的延长线于点C,若∠C=20°,求∠A的度数. 如图,已知∠AOC=∠BOD=90°,∠COD=38°,求∠AOB的度数.
如图,已知∠AOC=∠BOD=90°,∠COD=38°,求∠AOB的度数.
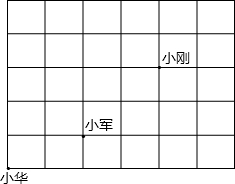 课间操时小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以用坐标表示成(4,3).
课间操时小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以用坐标表示成(4,3).