题目内容
11. 如图,AB是⊙O的直径,D是⊙O上一点,过点D作⊙O的切线交AB的延长线于点C,若∠C=20°,求∠A的度数.
如图,AB是⊙O的直径,D是⊙O上一点,过点D作⊙O的切线交AB的延长线于点C,若∠C=20°,求∠A的度数.
分析 连接OD,根据切线的性质得到OD⊥CD,由三角形的内角和得到∠DOC=70°,根据等腰三角形的性质得到∠A=∠ADO,根据圆周角定理即可得到结论.
解答  解:连接OD,
解:连接OD,
∵CD是⊙O的切线,
∴OD⊥CD,
∵∠C=20°,
∴∠DOC=70°,
∵OA=OD
∴∠A=∠ADO,
∵∠A+∠ADO=∠DOC=70°,
∴∠A=∠ADO=$\frac{1}{2}$∠DOC=35°.
点评 本题考查了切线的性质,三角形的内角和,圆周角定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
10.下列说法正确的是( )
| A. | 带根号的数一定是无理数 | |
| B. | 无限小数一定是无理数 | |
| C. | 无理数一定是无限小数 | |
| D. | 无理数是开平方或开立方开不尽的数 |
16.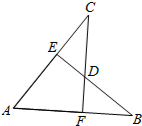 如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论错误的有( )个.
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论错误的有( )个.
 如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论错误的有( )个.
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论错误的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.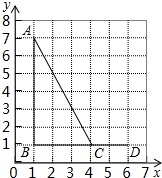 如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则下列坐标不可能是点E的坐标的是( )
如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则下列坐标不可能是点E的坐标的是( )
 如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则下列坐标不可能是点E的坐标的是( )
如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则下列坐标不可能是点E的坐标的是( )| A. | (4,0) | B. | (6,0) | C. | (6,4) | D. | (4,5) |
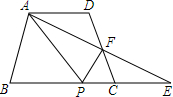 如图,在四边形ABCD中,AD∥BC,延长BC至点E,使CE=AD,连接AE交CD于点F,过点F作AE的垂线交BC于点P,连接PA.
如图,在四边形ABCD中,AD∥BC,延长BC至点E,使CE=AD,连接AE交CD于点F,过点F作AE的垂线交BC于点P,连接PA.
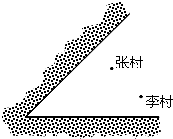 近年来,江苏省实施“村村通”工程和农村医疗卫生改革,宜兴市计划在某镇的张村、李村之间建一座定点医疗站P,张、李两村坐落在两相交公路内(如图所示),医疗站必须满足下列条件:①使其到两公路的距离相等;②到张、李两村的距离也相等.请你利用尺规作图确定P点的位置.(不写作法,保留作图痕迹)
近年来,江苏省实施“村村通”工程和农村医疗卫生改革,宜兴市计划在某镇的张村、李村之间建一座定点医疗站P,张、李两村坐落在两相交公路内(如图所示),医疗站必须满足下列条件:①使其到两公路的距离相等;②到张、李两村的距离也相等.请你利用尺规作图确定P点的位置.(不写作法,保留作图痕迹) ”,那么它的实际车牌号是:苏L27X37.
”,那么它的实际车牌号是:苏L27X37.