题目内容
有规律排列的一列数:2,-4,6,-8,10,-12,…
(1)它的每一项你认为可用怎样的式子来表示;
(2)它的第100个数是多少?
(3)2014是不是这列数中的数?如果是,是第几个数?
(1)它的每一项你认为可用怎样的式子来表示;
(2)它的第100个数是多少?
(3)2014是不是这列数中的数?如果是,是第几个数?
考点:规律型:数字的变化类
专题:
分析:(1)根据所给出的数据,找出规律,它的每一项可表示成(-1)n+1•2n(n是正整数),即可得出答案;
(2)根据(1)得出的规律,把n=100代入即可得出答案;
(3)根据(1)得出的规律,把n=1007代入,进行验证,即可得出答案.
(2)根据(1)得出的规律,把n=100代入即可得出答案;
(3)根据(1)得出的规律,把n=1007代入,进行验证,即可得出答案.
解答:解:(1)∵2=(-1)1+1•2×1,-4=(-1)2+1•2×2,6=(-1)3+1•2×3,…,
∴它的每一项用式子表示是:(-1)n+1•2n(n是正整数);
(2)当n=100时,(-1)100+1•2×100=-200;
(3)是;当这个数是1007时,
2014=(-1)1007+1×2×1007,成立,
则2014是这列数中的数.
∴它的每一项用式子表示是:(-1)n+1•2n(n是正整数);
(2)当n=100时,(-1)100+1•2×100=-200;
(3)是;当这个数是1007时,
2014=(-1)1007+1×2×1007,成立,
则2014是这列数中的数.
点评:此题考查了数字的变化类,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的关键规律为n=(-1)n+1•2n(n是正整数).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,把矩形纸片ABCD沿对角线折叠,若重叠部分为△EBD,那么下列说法错误的是( )
如图,把矩形纸片ABCD沿对角线折叠,若重叠部分为△EBD,那么下列说法错误的是( )| A、△EBD是等腰三角形 |
| B、折叠后得到的图形是轴对称图形 |
| C、折叠后∠ABE和∠CBD一定相等 |
| D、△EBA和△EDC一定全等 |
 如图,⊙A,⊙B,⊙C两两不相交,且半径都是1厘米,则图中三个扇形(即阴影部分)的面积之和为
如图,⊙A,⊙B,⊙C两两不相交,且半径都是1厘米,则图中三个扇形(即阴影部分)的面积之和为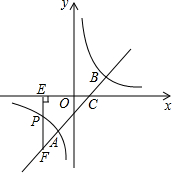 如图,直线y=x-1与反比例函数y=
如图,直线y=x-1与反比例函数y=
 如图:AB⊥BD,ED⊥BD,AB=CD,AC=CE.求证:AC⊥CE.
如图:AB⊥BD,ED⊥BD,AB=CD,AC=CE.求证:AC⊥CE.