题目内容
 如图,把矩形纸片ABCD沿对角线折叠,若重叠部分为△EBD,那么下列说法错误的是( )
如图,把矩形纸片ABCD沿对角线折叠,若重叠部分为△EBD,那么下列说法错误的是( )| A、△EBD是等腰三角形 |
| B、折叠后得到的图形是轴对称图形 |
| C、折叠后∠ABE和∠CBD一定相等 |
| D、△EBA和△EDC一定全等 |
考点:翻折变换(折叠问题)
专题:
分析:根据题意结合图形可以证明EB=ED,进而证明△ABE≌△CDE;此时可以判断选项A、B、D是成立的,问题即可解决.
解答: 解:由题意得:
解:由题意得:
△BCD≌△BFD,
∴DC=DF,∠C=∠F=90°;
∠CBD=∠FBD;
又∵四边形ABCD为矩形,
∴∠A=∠F=90°;DE∥BF,AB=DF;
∴∠EDB=∠FBD,DC=AB;
∴∠EDB=∠CBD,
∴EB=ED,△EBD为等腰三角形;
在△ABE与△CDE中,
∵
,
∴△ABE≌△CDE(HL);
又∵△EBD为等腰三角形,
∴折叠后得到的图形是轴对称图形;
综上所述,选项A、B、D成立,
∴下列说法错误的是C,
故选C.
 解:由题意得:
解:由题意得:△BCD≌△BFD,
∴DC=DF,∠C=∠F=90°;
∠CBD=∠FBD;
又∵四边形ABCD为矩形,
∴∠A=∠F=90°;DE∥BF,AB=DF;
∴∠EDB=∠FBD,DC=AB;
∴∠EDB=∠CBD,
∴EB=ED,△EBD为等腰三角形;
在△ABE与△CDE中,
∵
|
∴△ABE≌△CDE(HL);
又∵△EBD为等腰三角形,
∴折叠后得到的图形是轴对称图形;
综上所述,选项A、B、D成立,
∴下列说法错误的是C,
故选C.
点评:该命题主要考查了翻折变换及其应用问题;解题的关键是灵活运用翻折变换的性质,找出图中隐含的等量关系;借助矩形的性质、全等三角形的判定等几何知识来分析、判断、推理或解答.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
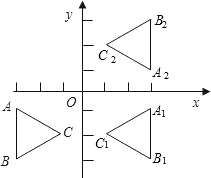 如图,直角坐标系中,△ABC为等边三角形,其中A、B、C的坐标分别为(-3,-1),(-3,-3),(-3+
如图,直角坐标系中,△ABC为等边三角形,其中A、B、C的坐标分别为(-3,-1),(-3,-3),(-3+
 如图:AD∥CB,AB∥CD,CF⊥BD,AE⊥BD,E、F是垂足,求证:AE=CF.
如图:AD∥CB,AB∥CD,CF⊥BD,AE⊥BD,E、F是垂足,求证:AE=CF.