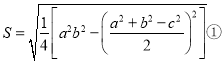Question

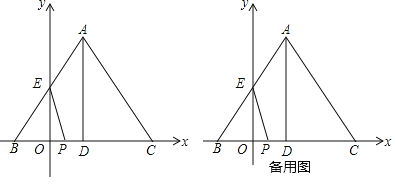
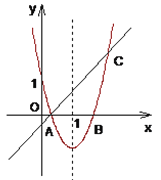
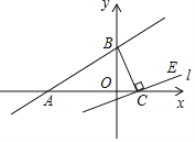
【题目】如图，一次函数y=kx+b（k≠0）的图象与x轴，y轴分别交于A（﹣9，0）、B（0，6），过点C（2，0）作直线l与BC垂直，点E在直线l位于x轴上方的部分．

（1）求一次函数y=kx+b（k≠0）的解析式；

（2）求直线l的解析式；

Answer 1

【答案】（1）y=x+6；（2）y=x﹣；

【解析】

（1）利用待定系数法求出直线表达式；

（2）记直线l与y轴的交点为D,再证明△OBC∽△OCD可得，由此可得D、C坐标，即可得直线l的解析式.

解：（1）∵一次函数y=kx+b（k≠0）的图象与x轴，y轴分别交于A（﹣9，0），B（0，6）两点，

∴

∴

∴一次函数y=kx+b的表达式为y=x+6；

（2）如图，记直线l与y轴的交点为D，

∵BC⊥l，

∴∠BCD=90°=∠BOC，

∴∠OBC+∠OCB=∠OCD+∠OCB，

∴∠OBC=∠OCD，

∵∠BOC=∠COD，

∴△OBC∽△OCD，

∴

∵B（0，6），C（2，0），

∴OB=6，OC=2，

∴

∴OD=

∴D（0，﹣），

∵C（2，0），

∴直线l的解析式为y=x﹣