题目内容
【题目】如图，已知抛物线
与x轴交于点A、B（点A在点B的左侧），与y轴交于C.
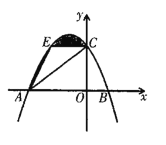
（1）求点A、B、C的坐标；
（2）若点E与点C关于抛物线的对称轴对称，求梯形AOCE的面积.
【答案】（1）A（-4,0），B（2,0），C,0,4）；（2）12
【解析】
（1）在抛物线的解析式中，令x=0可以求出点C的坐标，令y=0可以求出A、B点的坐标；（2）先求出E点坐标，然后求出OA，OC，CE的长计算面积即可.
解：（1）当y=0时，
-x+4=0，解得x1=－4，x2=2，
∴A（－4，0），B（2，0），当x=0时，y=4，∴C（0，4）；
（2）y=﹣x+4=
（x+1）2+
，
∴抛物线y=﹣x+4的对称轴是直线x=－1，
∴E的坐标为（－2，4），则OA=4，OC=4，CE=2，
S梯形AOCE=
练习册系列答案
相关题目
