题目内容
10.用正四边形和正八边形镶嵌成一个平面,则在某一个顶点处,正四边形和正八边形的个数分别为( )| A. | 2个和1个 | B. | 1个和2个 | C. | 3个和1个 | D. | 1个和3个 |
分析 利用正多边镶嵌的条件,结合各个正多边形的每个内角的度数即可求出答案.
解答 解:正八边形内角为135°,(360-90)÷135=2,所以一个顶点周围应该有两个正八边形,一个正四角形.
故选B.
点评 本题考查了两个正多边形平整镶嵌的条件:这两个正多边形的内角的整数倍的和为360°,同时也考查了正多边形内角的计算方法.

练习册系列答案
相关题目
20.已知一个阿米巴虫的质量约是0.000005克,下面用科学计数法表示一个阿米巴虫的质量.其中正确的是( )
| A. | 5.0×10-6克 | B. | 5.0×106克 | C. | 5.0×10-5克 | D. | 5.0×105 |
1.下列命题中,真命题是( )
| A. | 对角线互相垂直且相等的四边形是菱形 | |
| B. | 有一组邻边相等的平行四边形是菱形 | |
| C. | 对角线互相平分且相等的四边形是菱形 | |
| D. | 对角线相等的四边形是菱形 |
15.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. | 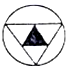 |
2.为了参加中学生篮球运动会,某校篮球队准备购买10双运动鞋,经统计10双运动鞋尺码(cm)如表所示:
则这10双运动鞋的众数和中位数分别为( )
| 尺码 | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量(双) | 2 | 4 | 2 | 1 | 1 |
| A. | 25.5 cm 26 cm | B. | 26 cm 25.5 cm | C. | 26 cm 26 cm | D. | 25.5 cm 25.5 cm |